LabDSV: Classification Tree Models

Lab 6 --- Classification Tree Models

As the final species modeling method we will use classification trees. Tree classifiers are often called CART (for Classification And Regression Trees), but CART is actually a specific (copyrighted and trade-marked) example of such approaches. R contains two different implementations of tree classifiers, tree() in package tree, and rpart() in package rpart. Due to its similarity to GLM and GAM (deviance-based) the material below is based on tree().

Tree Classifiers

To use the tree() function we use an approach similar to the glm() function, i.e. a formula with a dependent variable and independent (predictor) variables on the right. Tree classifiers are called "tree" classifiers because their result is a dichotomous key that resembles a tree. Because ecologists are generally extremely familiar with dichotomous keys from taxonomy, the result seems quite intuitive.

To demonstrate tree classifiers we will start with the very simple example we used for GLM.

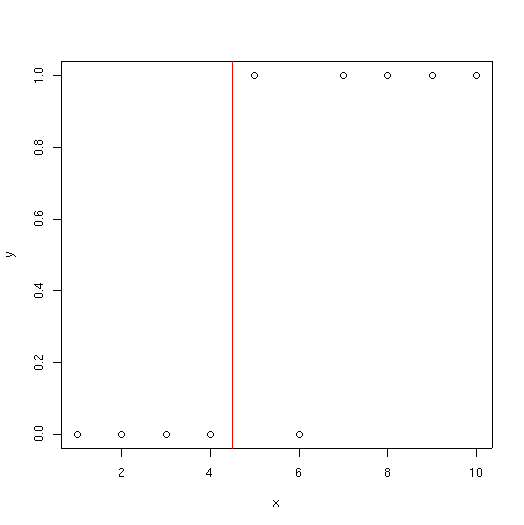
x <- 1:10
y <- c(0,0,0,0,1,0,1,1,1,1)
plot(x,y)

As you can see, at low values of x, species y is usually absent; at high values of x it is usually present. With a tree classifier, we try and find a series of splits that separates the presences from absences. In this example the dataset is artificially small; tree() usually will not produce splits smaller than 5 samples. So to make things work on this example we have to override some of the defaults as shown below.

test <- tree(factor(y)~x,control=tree.control(nobs=10,mincut=3))

Notice that in contrast to GLM or GAM we did not have to specify a family=binomial, but we did have to surround the dependent variable with factor(). That tells tree() that we want a logistic, or classification, tree rather than a regression tree. Normally, we do not need to use the control=tree.control() function inside the call to tree(). It was only necessary here because the dataset was so small.

To see the tree simply type its name.

test

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

1) root 10 13.860 0 ( 0.5000 0.5000 )
  2) x < 4.5 4  0.000 0 ( 1.0000 0.0000 ) *
  3) x > 4.5 6  5.407 1 ( 0.1667 0.8333 ) *

At each branch of the tree (after the root) we see in order:

the branch number (e.g. 2))
the split (e.g. x < 4.5)
the number of samples going along that split (e.g. 4)
the deviance associated with that split (e.g. 0.000)
the predicted value (e.g. 0=absent)
the fraction of samples in that branch that are absent and present (e.g. ( 1.0000 0.0000 ))
and, IF it is a terminal node (or leaf), a "*"

The "root" node is equivalent to the null deviance model in GLM or GAM; if you made no splits, what would the deviance be? In this case we have 5 presences and 5 absences, so

$$ -2 \times \Bigl(n_i \times log(n_i/N) + (N-n_i) \times log\bigl((N-n_i)/N\bigl)\Bigr) $$

-2 * 10 * log(0.5) = 13.86

The second branch has 4 samples, all absences, so the deviance associated with it is 0.

2) x < 4.5 4 0.000 0 ( 1.0000 0.0000 ) *

The tree keeps splitting "nodes" or branch points to make the resulting branches or leaves more "pure" (lower deviance).

There is a summary function associated with trees.

summary(test)

Classification tree:
tree(formula = factor(y) ~ x, control = tree.control(nobs = 10,
    mincut = 3))
Number of terminal nodes:  2
Residual mean deviance:  0.6758 = 5.407 / 8
Misclassification error rate: 0.1 = 1 / 10

The summary() function shows

the formula
the number of terminal nodes
the residual mean deviance (along with residual deviance)
the misclassification error rate

The following plot shows the split identified by the tree.

Real Data

Now that you understand the mechanics, let's do a more realistic example. Assuming we have both bryceveg and brycesite attached, let's continue our efforts to model Berberis repens.

demo <- tree(factor(berrep>0)~elev+slope+av)
summary(demo)

Classification tree:
tree(formula = factor(berrep > 0) ~ elev + slope + av)
Number of terminal nodes:  15
Residual mean deviance:  0.4907 = 71.15 / 145
Misclassification error rate: 0.1125 = 18 / 160

 demo

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 160 218.200 FALSE ( 0.57500 0.42500 )
   2) elev < 8020 97  80.070 FALSE ( 0.85567 0.14433 )
     4) slope < 20 89  62.550 FALSE ( 0.88764 0.11236 )
       8) slope < 2.5 35  39.900 FALSE ( 0.74286 0.25714 )
        16) av < 0.785 22  28.840 FALSE ( 0.63636 0.36364 )
          32) elev < 7660 11  15.160 TRUE ( 0.45455 0.54545 )
            64) elev < 7370 6   7.638 FALSE ( 0.66667 0.33333 ) *
            65) elev > 7370 5   5.004 TRUE ( 0.20000 0.80000 ) *
          33) elev > 7660 11  10.430 FALSE ( 0.81818 0.18182 )
            66) av < 0.455 6   0.000 FALSE ( 1.00000 0.00000 ) *
            67) av > 0.455 5   6.730 FALSE ( 0.60000 0.40000 ) *
        17) av > 0.785 13   7.051 FALSE ( 0.92308 0.07692 ) *
       9) slope > 2.5 54   9.959 FALSE ( 0.98148 0.01852 )
        18) av < 0.7 36   0.000 FALSE ( 1.00000 0.00000 ) *
        19) av > 0.7 18   7.724 FALSE ( 0.94444 0.05556 )
          38) elev < 7490 5   5.004 FALSE ( 0.80000 0.20000 ) *
          39) elev > 7490 13   0.000 FALSE ( 1.00000 0.00000 ) *
     5) slope > 20 8  11.090 FALSE ( 0.50000 0.50000 ) *
   3) elev > 8020 63  51.670 TRUE ( 0.14286 0.85714 )
     6) av < 0.055 7   9.561 TRUE ( 0.42857 0.57143 ) *
     7) av > 0.055 56  38.140 TRUE ( 0.10714 0.89286 )
      14) av < 0.835 36   9.139 TRUE ( 0.02778 0.97222 )
        28) av < 0.215 8   6.028 TRUE ( 0.12500 0.87500 ) *
        29) av > 0.215 28   0.000 TRUE ( 0.00000 1.00000 ) *
      15) av > 0.835 20  22.490 TRUE ( 0.25000 0.75000 )
        30) av < 0.965 12  16.300 TRUE ( 0.41667 0.58333 )
          60) slope < 2.5 6   7.638 FALSE ( 0.66667 0.33333 ) *
          61) slope > 2.5 6   5.407 TRUE ( 0.16667 0.83333 ) *
        31) av > 0.965 8   0.000 TRUE ( 0.00000 1.00000 ) *

Notice how the same variables are used multiple times, often repeatedly in a single branch

plot(demo)
text(demo)

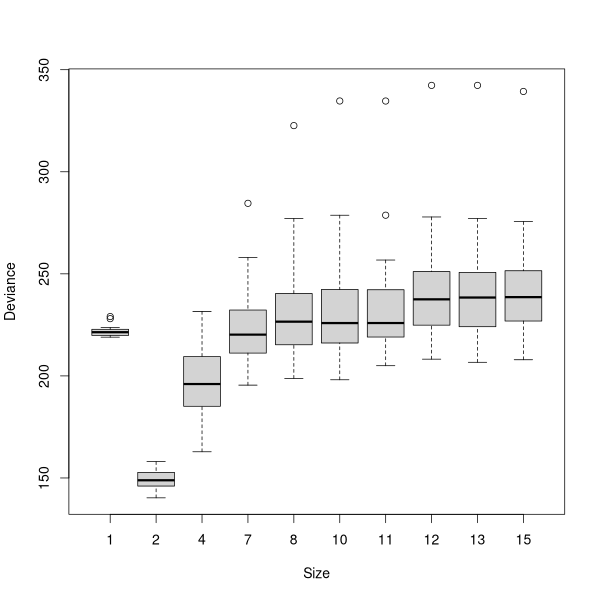
The height of the vertical lines in the plot is proportional to the reduction in deviance, so not all lines are equal, and you can see the important ones immediately.

Cross-validation

Unfortunately, tree-classifiers tend to over-fit their models extremely. Unlike GLM and GAM models where we can use the reduction in deviance compared the the number of degrees of freedom to test for significance, with tree classifiers we need to go to another approach. The generally used approach is 10-fold cross-validation, where 10% of the data are held out, a tree is fit to the other 90% of the data, and the held-out data are dropped through the tree. While doing so, we note at what level the tree gives the best results. Then we hold out a different 10% and repeat. Fortunately, the whole thing is automated with the cv.tree() function. To perform cross-validation, simple execute the cv.tree function with your tree as the argument to the function. E.g.

demo.cv <- cv.tree(demo)

and then plot the result. E.g.

plot(demo.cv)

The curve (or jagged line) shows where the minimum deviance occurred with the cross-validated tree. Many people find these curves difficult to evaluate, as the stair-step curve seems ambiguous for a single value. For example, what is the value for X=4, ~150, or ~ 180? These curves are read as the last point along the line or any given X: thus at X=2, Y=147, not 220, and at X=4, Y=180, not 147.

In this case, the best tree would appear to be 2-3 terminal nodes. Actually, there was no test for 3 terminal nodes, only 2 and 4, so the straight line from 2 to 4 is a little misleading. So, we'll get the best tree with two terminal nodes.

The results of a cross-validation are stochastic, and every time you run the cv.tree() function you will get somewhat different results. To finesses this problem, the multi.cv() function (see below) can be used to generate a boxplot of results. multi.cv(demo) To prune the tree, we use the prune.tree() function with a best=n argument, where n = the number of terminal nodes we want.

demo.x <- prune.tree(demo,best=2)

This "pruned" tree is a tree object just like the others, and can be plotted or summarized.

plot(demo.x)
text(demo.x)

demo.x

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

1) root 160 218.20 FALSE ( 0.5750 0.4250 )  
  2) elev < 8020 97  80.07 FALSE ( 0.8557 0.1443 ) *
  3) elev > 8020 63  51.67 TRUE ( 0.1429 0.8571 ) *

summary(demo.x)

Classification tree:
snip.tree(tree = demo, nodes = c(3, 2))
Variables actually used in tree construction:
[1] "elev"
Number of terminal nodes:  2 
Residual mean deviance:  0.8338 = 131.7 / 158 
Misclassification error rate: 0.1438 = 23 / 160

In comparison to our original tree, this summary also has a list of variables actually used. In GLM or GAM every variable was used, but in tree classifiers a variable is only used if it is the best available variable, and especially in pruned trees many variables never enter the model. In this case, only elev was used.

In addition, note that the misclassification rate has gone up significantly. The previous number was an optimistic over-fit number; this one is much more realistic.

As you can see, the tree is remarkably simple with only two terminal nodes. Surprisingly, it's fairly accurate. As you might remember from Lab 4, our GLM model achieved an accuracy of 0.85, whereas our tree achieves 0.856 (more or less the same, but an improvement of 1 plot correctly classified out of 160).

Arguably, based on parsimony, we would want the smallest tree that has minimum cross-validated deviance. As a special case, if the minimum deviance occurs with a tree with 1 node, then none of your models are better than random, although some might be no worse. Alternatively, in an exploratory mode, we might want the most highly-resolved tree that is among the trees with lowest deviance (as long as that does not include the null tree with one node). For the sake of example, lets go with a four node tree.

demo.x <- prune.tree(demo,best=4)
demo.x

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

1) root 160 218.200 FALSE ( 0.57500 0.42500 )
  2) elev < 8020 97  80.070 FALSE ( 0.85567 0.14433 )
    4) slope < 20 89  62.550 FALSE ( 0.88764 0.11236 )
      8) slope < 2.5 35  39.900 FALSE ( 0.74286 0.25714 ) *
      9) slope > 2.5 54   9.959 FALSE ( 0.98148 0.01852 ) *
    5) slope > 20 8  11.090 FALSE ( 0.50000 0.50000 ) *
  3) elev > 8020 63  51.670 TRUE ( 0.14286 0.85714 ) *

summary(demo.x)

Classification tree:
snip.tree(tree = demo, nodes = c(9, 8, 3))
Variables actually used in tree construction:
[1] "elev"  "slope"
Number of terminal nodes:  4
Residual mean deviance:  0.722 = 112.6 / 156
Misclassification error rate: 0.1438 = 23 / 160

Notice that while the residual deviance decreased a little (0.722 vs 0.834), the classification accuracy did not improve at all (23/160 misclassified). Despite the apparent increase in detail of the tree, it's arguably actually no better.

Categorical Variables

Just like we did in GLM and GAM, we can use categorical variables in the model as well. However, instead of having a regression coefficient for all but the contrast, we try to find the best way to split the categories into two sets. If a variable has k categories, the number of ways to split it is 2^(k-1) - 1, so be careful with variables with numerous categories.

Let's try an example with topographic position, this time using Arctostaphylos patula.

demo.2 <- tree(factor(arcpat>0)~elev+slope+pos)
demo.2

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 160 220.900 FALSE ( 0.53750 0.46250 )
   2) elev < 7980 96 105.700 FALSE ( 0.76042 0.23958 )
     4) elev < 6930 14   0.000 FALSE ( 1.00000 0.00000 ) *
     5) elev > 6930 82  97.320 FALSE ( 0.71951 0.28049 )
      10) elev < 7460 26  35.890 TRUE ( 0.46154 0.53846 )
        20) pos: ridge,up_slope 12  13.500 FALSE ( 0.75000 0.25000 ) *
        21) pos: bottom,low_slope,mid_slope 14  14.550 TRUE ( 0.21429 0.78571 ) *
      11) elev > 7460 56  49.380 FALSE ( 0.83929 0.16071 )
        22) slope < 2.5 22  28.840 FALSE ( 0.63636 0.36364 )
          44) elev < 7845 12  16.300 TRUE ( 0.41667 0.58333 )
            88) pos: mid_slope,ridge 6   7.638 FALSE ( 0.66667 0.33333 ) *
            89) pos: bottom,low_slope,up_slope 6   5.407 TRUE ( 0.16667 0.83333 ) *
          45) elev > 7845 10   6.502 FALSE ( 0.90000 0.10000 ) *
        23) slope > 2.5 34   9.023 FALSE ( 0.97059 0.02941 )
          46) elev < 7890 24   0.000 FALSE ( 1.00000 0.00000 ) *
          47) elev > 7890 10   6.502 FALSE ( 0.90000 0.10000 ) *
   3) elev > 7980 64  64.600 TRUE ( 0.20312 0.79688 ) *

multi.cv(demo.2)

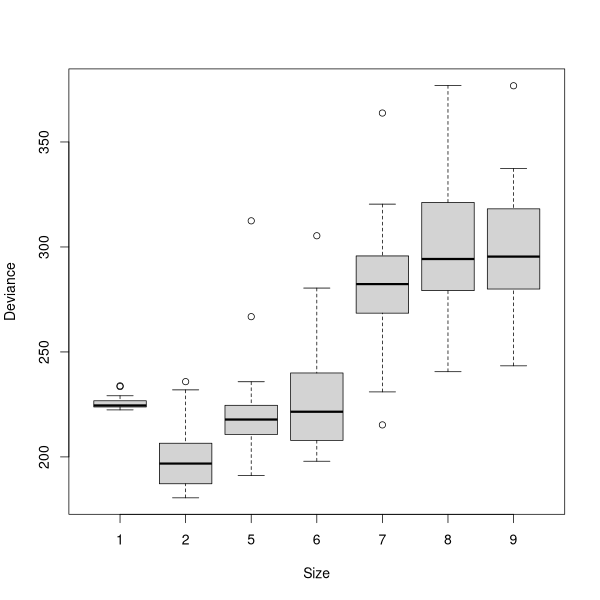
For the sake of exploration I'm going to go with a slightly more complicated tree than indicated bt cross-validation.

demo2.x <- prune.tree(demo.2,best=5)
plot(demo2.x)
text(demo2.x)

demo2.x

node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 160 220.900 FALSE ( 0.53750 0.46250 )
   2) elev < 7980 96 105.700 FALSE ( 0.76042 0.23958 )
     4) elev < 6930 14   0.000 FALSE ( 1.00000 0.00000 ) *
     5) elev > 6930 82  97.320 FALSE ( 0.71951 0.28049 )
      10) elev < 7460 26  35.890 TRUE ( 0.46154 0.53846 ) *
      11) elev > 7460 56  49.380 FALSE ( 0.83929 0.16071 )
        22) slope < 2.5 22  28.840 FALSE ( 0.63636 0.36364 ) *
        23) slope > 2.5 34   9.023 FALSE ( 0.97059 0.02941 ) *
   3) elev > 7980 64  64.600 TRUE ( 0.20312 0.79688 ) *

summary(demo2.x)

Classification tree:
snip.tree(tree = demo.2, nodes = c(23, 22, 10))
Variables actually used in tree construction:
[1] "elev"  "slope"
Number of terminal nodes:  5
Residual mean deviance:  0.8926 = 138.4 / 155
Misclassification error rate: 0.2125 = 34 / 160

Notice how in the pruned tree, pos no longer appears; all the splits employing pos were pruned off. Notice also that the error rate has increased significantly for arcpat compared to berrep (34/160 vs 23/160). Apparently, arcpat has a more complicated distribution, or responds to variables other than elev and slope more than does berrep.

Regression Trees

Just as we could use family='poisson' in GLM and GAM models to get estimates of abundance, rather than presence/absence, we can run the tree() function in regression mode, rather than classification mode. We do not have to specify a family argument, however. If the dependent variable is numeric, tree will automatically produce a regression tree (this actually trips up quite a few users who have numeric categories and forget to surround their dependent variable with factor()).

So, lets detach our bryceveg data frame, and attach the cover-class midpoint data frame from Lab 1.

detach(bryceveg)
attach(cover)

Now, we'll try and estimate arcpat's abundance with a regression tree.

demo.3 <- tree(arcpat~elev+slope+pos)
demo.3

node), split, n, deviance, yval
      * denotes terminal node

  1) root 160 101800.0 14.600
    2) elev < 7910 90  33000.0  7.289
      4) slope < 20 83  26870.0  5.795
        8) slope < 2.5 33  22500.0 12.940
         16) elev < 7370 12    203.1  1.375 *
         17) elev > 7370 21  19780.0 19.550
           34) elev < 7690 6   5243.0 55.420 *
           35) elev > 7690 15   3726.0  5.200 *
        9) slope > 2.5 50   1574.0  1.080 *
      5) slope > 20 7   3750.0 25.000 *
    3) elev > 7910 70  57810.0 24.000
      6) elev < 8650 53  48230.0 28.460
       12) pos: bottom,low_slope,up_slope 19  11240.0 15.510 *
       13) pos: mid_slope,ridge 34  32020.0 35.690
         26) elev < 8135 7   6373.0 18.000 *
         27) elev > 8135 27  22890.0 40.280
           54) elev < 8325 8   6000.0 60.000 *
           55) elev > 8325 19  12470.0 31.970
            110) slope < 2.5 6   1710.0 13.670 *
            111) slope > 2.5 13   7820.0 40.420
              222) elev < 8490 5   2938.0 27.500 *
              223) elev > 8490 8   3526.0 48.500 *
      7) elev > 8650 17   5258.0 10.120 *

Here, instead of having a list of probabilities of occurrence, the terminal value at each node is the estimated percent cover of arcpat. For example, the root node says the overall mean abundance of arcpat is 14.6 percent. This is of course the same value we would get from

mean(arcpat)

[1] 14.60125

Following the splits, the first terminal node is 16, where the estimated abundance of arcpat that has elev < 7370 and slope < 2.5 (collapsing the tree) is 1.375 percent.

Exactly as we did for classification trees, we can cross-validate the regression tree as well.

multi.cv(demo.3)

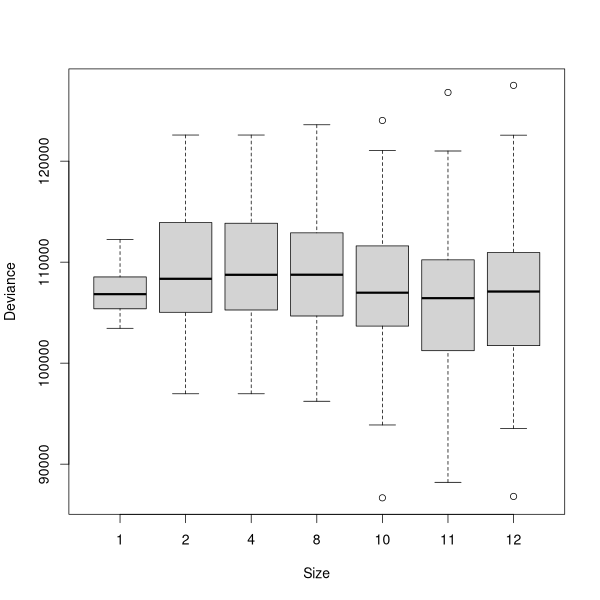
demo3.x <- prune.tree(demo.3,best=11)
summary(demo3.x)

Regression tree:
snip.tree(tree = demo.3, nodes = 111)
Number of terminal nodes:  11
Residual mean deviance:  355 = 52900 / 149
Distribution of residuals:
      Min.    1st Qu.     Median       Mean    3rd Qu.       Max.
-6.000e+01 -7.118e+00 -1.080e+00  1.588e-15 -5.626e-01  6.949e+01

Notice how for a regression tree the summary lists the distribution of residuals, rather than a classification error rate. The errors are quantitative, exactly as for a Poisson regression with a GLM or GAM.

Random Forest or randomForest

Random Forest is an algorithm based on classification trees. The idea is to use "bagging" (bootstrapped permutations of the data) to better estimate the model and in particular to reduce over-fitting of the model. Ransom Forest employs a classification tree based on the Gini index, not deviance, so it's a little different than what we have explored so far. The particular version we use in R is an appropriation (slighly loaded word) of the original code by Breiman and Cutler (Breiman 2001), ported to R by Liaw Wiener (2002) The package is called randomForest (reportedly because that was the sole permutation of "Random" and "Forest" that Breiman and Cutler didn't trademark). The Random Forest algorithm:

splits the data into training and "out-of-bag" (or validation),
chooses a subset of predictor(or explanatory) variables randomly, and
fits a large number of models.

Explanatory variable are tracked across replicates to see which variables reduce the Gini index the most (have the largest effect size). The final model is an amalgam of the votes of the replicates, and not an actual single tree. There are numerous arguments to the randomForest function differing in defaults for classification versus regression. For our purposes, to fit a predictive model of presence/absence for Berberis repens the dfefaults are:

fits 500 trees,
chooses N sam,ple plots with replacement,
chooses $\sqrt(p)$ explanatory variables where $p$ is the number of explanatory variable in the formula,
splits down to a terminal node size of 1

There is no maximum tree size set by default. The algorithm then classifies the "out-of-bag" samples for each of the 500 trees, pruning back to maximum cross-validated reduction in the Gini index. To run the algorithm in R, first load the randomForest package.

library(randomForest) # note the Camelcase

Then, following the above, let's fit a predictive model for presence/absence of Berberis repens using elevation, aspect value, and slope

berrep.rf <- randomForest(factor(berrep>0) ~ ~ elev + slope + av) berrep.rf

Call: randomForest(formula = factor(berrep > 0) ~ elev + slope + av) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 1 OOB estimate of error rate: 15.62% Confusion matrix: FALSE TRUE class.error FALSE 82 10 0.1086957 TRUE 15 53 0.2205882

The default print() function produces a copy of the function call, the number of trees fitted, the number of variables/tree, the out-of-bag error estimate, and a confusion matrix. There is no tree to visualize (optionally you can save all 500 and look at them all keep.forest=TRUE). For a simple presence/absence model the output is pretty simple, especially if you fit as few explanatory variables as I did. Nonetheless it's better than we achieved with the tree classifier (15.62% versus 21.25%). randomForets has a nice visualization of variable effect size.

varImpPlot(berrep.rf) # note the camelCase

You can immediately see that elevation is three- to four-fold more important than aspect value (av) or slope. To show the variable selection aspects of randomForest and give perhaps a more realistic example I'll fit another model with more explanatory variables.

berrep_2.rf <- randomForest(factor(berrep>0) ~ annrad + av + elev + grorad + pos + slope)

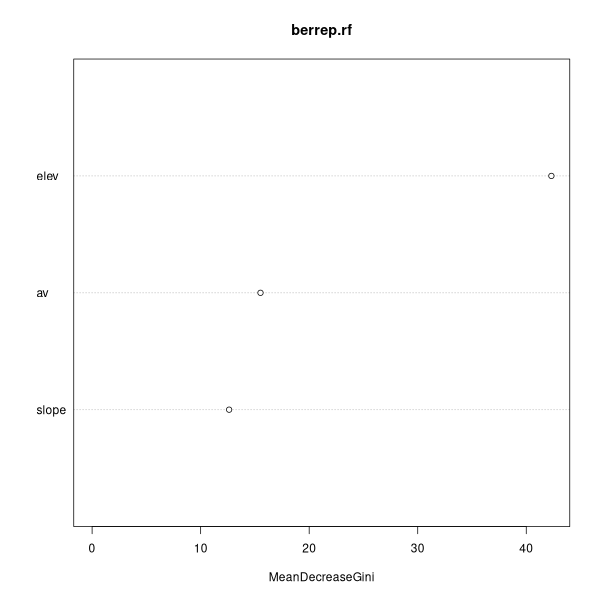
Call:
 randomForest(formula = factor(berrep > 0) ~ 
               annrad + av + elev + grorad + pos + slope)

               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 20.62%
Confusion matrix:
      FALSE TRUE class.error
FALSE    78   14   0.1521739
TRUE     19   49   0.2794118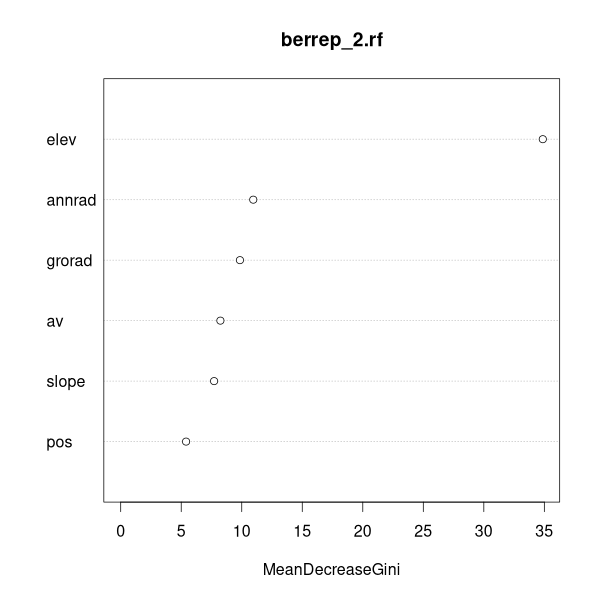

Surprisingly, the results got worse! Unlike the tree classifier that only selects variables that help, randomForest() random selects sets of all variables (in this case of size 2), so some trees are made from poor variables. To see which variables SHOULD be included, go back to the plot.

varImpPlot(berrep_2.rf)

Maybe a model with elev, grorad and annrad would be best.

berrep_3_rf <- randomForest(factor(berrep>0) ~ elev + grorad + annrad) berrep_3_rf

Call: randomForest(formula = factor(berrep > 0) ~ elev + grorad + annrad) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 1 OOB estimate of error rate: 19.38% Confusion matrix: FALSE TRUE class.error FALSE 76 16 0.1739130 TRUE 15 53 0.2205882

Nope, still slightly worse than our first model. Like classification trees, randomForest can also be run in regression mode if the dependent variable is quantitative.

Helpful Functions

multi.cv <- function (tree,n=20) { x <- cv.tree(tree)$size cv <- matrix(0,nrow=n,ncol=length(x)) for (i in 1:n) { cv[i,] <-rev( cv.tree(tree)$dev) } boxplot(cv,names=rev(as.character(x)), xlab='Size',ylab='Deviance') }

varImpPlot.tree <- function (tree,progress=FALSE) { x <- tree$frame x$leaf <- as.numeric(row.names(x)) delta <- rep(0,nrow(x)) devs <- rep(0,nlevels(x$var)) names(devs) <- as.character(levels(x$var)) for (i in 1:nrow(x)) { if (x$var[i] != '') { stem <- x$leaf[i] delta[i] <- x$dev[i] - (x$dev[x$leaf==stem*2] + x$dev[x$leaf==stem*2+1]) pnt <- which(levels(x$var)==x$var[i]) devs[pnt] <- devs[pnt] + delta[i] if (progress) cat(c(as.character(x$var[i]),round(delta[i],3),'\n')) } } dotchart(sort(devs[devs>0]),xlab='Deviance Explained') invisible(devs) }

References

Breiman, L. (2001), _Random Forests_, Machine Learning 45(1), Liaw A., and M. Wiener (2002). Classification and Regression by randomForest. R News 2(3), 18--22. 5-32.