LAB 14 --- Discriminant Analysis with Tree Classifiers

In Lab 13 we classified our vegetation into discrete "clusters" based strictly on vegetation composition using a variety of classification algorithms. The objective of these classification efforts was to produce classes that were internally homogeneous and distinct from the other clusters. We measured the success of these efforts using a variety of measures, including within-cluster/among-cluster similarity ratios and mean silhouette widths.

In this lab we want to know the degree to which plot membership in a cluster is predictable from environmental variables not used in the classification. There are several reasons we might want to pursue this effort. Similar to our efforts with fitting surfaces on ordinations, one important reason is to determine the relationship between environmental variability and vegetation composition. Here we approaching the question with a less continuous variability. More important than interpretation, however, is the potential for prediction. That is, given environmental variables, can we predict vegetation composition? Back in Labs 4 and 5 we tried to predict the presence/absence or abundance of single species, but here we're predicting total community composition within classes or types. Specifically, rather than try to predict a single value (presence or abundance), we're trying choose among a set of possible alternatives. Every plot must be assigned to a type.

Among the variety of techniques available to us (e.g. linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA)) in this lab we will emphasize tree-based classifiers. Tree classifiers are often called CART (for Classification And Regression Trees), but CART is actually a specific (copyrighted and trade-marked) example of such approaches. In R the tree classifier is called tree() To get started, we need to load somae packages. 

library(optpart)
library(tree)
data(brycesite)
data(bryceveg)
attach(brycesite)

Example Classifications

For the sake of demonstration I will create two cluster analyses from the Bray/Curtis dissimilarity matrix we created several labs ago. The first is a hierarchical cluster analysis using the "complete" or furthest neighbor algorithm. 
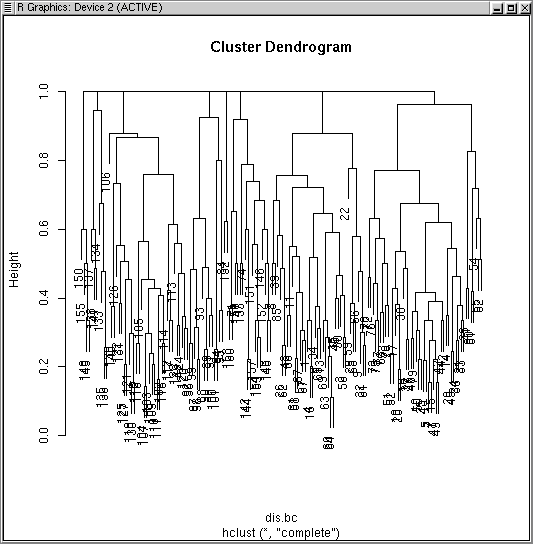
hcl1 <- hclust(dis.bc,method="complete")
plot(hcl1)

As we've seen before, using the "complete" method leads to discrete clusters at 1.0 dissimilarity. I'll slice the tree at 0.99 to generate clusters. 

hcl1.99 <- cutree(hcl1,h=0.99)
table(hcl1.99)

 1  2  3  4  5  6  7  8 
38 46 17  2 14 32  7  4
The result is eight clusters, with three of them (4, 7, and 8) being rather small. Our second demonstration clustering is an optpart into 5 clusters. 
opt5 <- optpart(5,dis.bc)
table(opt5$clustering)

 1  2  3  4  5 
38 92 14 12  4
The result is five clusters (as requested) although one (5) is rather small.

Tree Classifiers

To use the tree() function we use an approach similar to the glm() function, i.e. a formula with a dependent variable and independent (predictor) variables on the right. Assuming that the site dataframe is attached,
tree1 <- tree(factor(hcl1.99) ~ elev + av + slope + depth + pos)
The factor(hcl1.99) conversion is required so that the tree() function will recognize hcl1.99 as a categorical variable rather than numeric. The tree can be plotted and labeled with the following sequence: 
plot(tree1)
text(tree1)

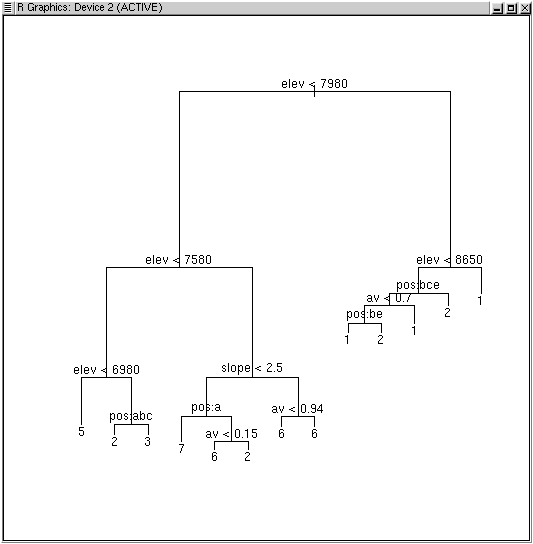
The tree is shown with the root at the top, and each sequential split along each branch is labeled with the respective criterion for splitting. Values that are true go left; values that are false go right. The height of the vertical bar above each split reflects the decrease in deviance associated with that split. To see the output, just type it's name.

tree1
node), split, n, deviance, yval, (yprob) * denotes terminal node 1) root 145 501.900 2 ( 0.25517 0.27586 0.08966 ... 0.04828 0.01379 ) 2) elev < 7980 83 273.200 6 ( 0.00000 0.18072 ... 0.08434 0.02410 ) 4) elev < 7580 34 87.550 3 ( 0.00000 0.14706 ... 0.00000 0.05882 ) 8) elev < 6980 14 7.205 5 ( 0.00000 0.00000 ... 0.00000 ) * 9) elev > 6980 20 41.320 3 ( 0.00000 0.25000 ... 0.05000 0.10000 ) 18) pos: bottom,low_slope,mid_slope 8 19.410 2 ( ... 0.12500 ) * 19) pos: ridge,up_slope 12 13.590 3 ( 0.00000 ... 0.08333 ) * 5) elev > 7580 49 95.200 6 ( 0.00000 0.20408 00000 ... 0.00000 ) 10) slope < 2.5 20 48.230 2 ( 0.00000 0.40000 ... 0.00000 ) 20) pos: bottom 8 6.028 7 ( 0.00000 0.12500 ... 0.00000 ) * 21) pos: low_slope,mid_slope,ridge,up_slope 12 21.300 2 ( ...) 42) av < 0.15 5 9.503 6 ( 0.00000 0.20000 ... 0.00000 ) * 43) av > 0.15 7 5.742 2 ( 0.00000 0.85714 ... 0.00000 ) * 11) slope > 2.5 29 14.560 6 ( 0.00000 0.06897 ... 0.00000 ) 22) av < 0.94 24 0.000 6 ( 0.00000 0.00000 ... 0.00000 ) * 23) av > 0.94 5 6.730 6 ( 0.00000 0.40000 ... 0.00000 ) * 3) elev > 7980 62 83.610 1 ( 0.59677 0.40323 ... 0.00000 ) 6) elev < 8650 45 61.830 2 ( 0.44444 0.55556 ... 0.00000 0.00000 ) 12) pos: low_slope,mid_slope,up_slope 38 52.570 1 ( 0.52632 ... ) 24) av < 0.7 22 25.780 2 ( 0.27273 0.72727 0.00000 ... 0.00000 ) 48) pos: low_slope,up_slope 8 10.590 1 ( 0.62500 ... 0.00000 ) * 49) pos: mid_slope 14 7.205 2 ( 0.07143 0.92857 ... 0.00000 ) * 25) av > 0.7 16 12.060 1 ( 0.87500 0.12500 0.00000 ... 0.00000 ) * 13) pos: ridge 7 0.000 2 ( 0.00000 1.00000 0.00000 ... 0.00000 ) * 7) elev > 8650 17 0.000 1 ( 1.00000 0.00000 0.00000 ... 0.00000 ) *
That takes a little explaining (and a little shoehorning to fit, the ellipses represent class probabilities I've deleted to make it fit). The tree is a dichotomous key (just like for plant or animal taxa). The first line is the root node (or trunk of the tree) which says that Looking at the first two branches (2 and 3), the maximum probability on branch 2 is for cluster 6 = 0.37349 with 83 pots going that way. Had we followed branch 3, Note that the sum of the respective deviances is less than the null deviance, i.e. 273.200 + 83.610 < 501.900. In fact, we achieved a reduction in deviance of 501.90 - (273.200+83.610) = 145.09 with a single split. The objective of the tree classifier is to minimize the deviance of the tree with each split, and the optimal split is calculated by comparing reduction in deviance. No other possible split in these data would have achieved as significant a reduction in deviance as achieved here.

Once we split, we simply proceed with the same objective independently for each branch on the remaining data. For example, on branch 2, where we now have 83 plots, the next split is 

  4) elev < 7580 34  87.550 3 ( 0.00000 0.14706 0.38235 ... 0.00000 0.05882)
  5) elev > 7580 49  95.200 6 ( 0.00000 0.20408 0.00000 ... 0.14286 0.00000)
Branches continue splitting until (1) they become pure, or (2) they become too small to split. In the R version, the minimum "terminal node" size is 10, and the minimal number of plots to be split off is 5. Once the tree is finished splitting, terminal nodes are designated with an asterisk at the end of the probability vector, e.g. nodes 8, 18, and 19 in the tree above. Terminal nodes are equivalent to coming to the identification of a species in a taxonomic key, and predict the type for all sample in that node.

To see a simple summary of the results, enter

summary(tree1)
Classification tree:
tree(formula = factor(hcl1.99) ~ elev + av + slope + depth + 
    pos)
Variables actually used in tree construction:
[1] "elev"  "pos"   "slope" "av"   
Number of terminal nodes:  13 
Residual mean deviance:  0.7428 = 98.05 / 132 
Misclassification error rate: 0.131 = 19 / 145
Several important pieces of information are given here. So, first things first. If we gave the classifier five variable to use, why did it only use four? At each split the best variable (maximum reduction in deviance) is used, and a single variable is often used more than once. In the example tree, soil depth deep was never used, and so was dropped from the analysis. On the other hand, elev was used repeatedly.

If there are eight types, why are there 13 terminal nodes? For some types there is more than one route to a terminal node. For example, nodes 22, 23, and 42 all predict cluster 6. Nodes 22 and 23 are a single split, and yet both predict cluster 6. Why is that? Node 22 predicts type 6 perfectly (p=1.0, dev.=0) while node 23 is less clean (p=0.60, dev.=6.73). Splitting node 11 into 22 and 23 achieved a reduction in deviance of 14.560 - (6.730+0.000) = 7.83 with a single split, even though both branches predicted the same type. Less obvious at first glance, is that some types or clusters were never predicted at all. None of the terminal nodes predicts types 4 or 8. There are simply too few plots in those types to predict accurately, and they fall below the minimum splitting rule of at least 5 plots/type.

The misclassification error is 19 out of 145, or 0.131 or 13%. That's good enough for practical purposes probably. We could calculate a probability of getting 126/145 correct given our initial distribution, but it's bound to be very significant. Of more interest perhaps is which types were confused with which other types. We can view this in a table called a "confusion matrix." In package optpart there is a confusion matrix function called confus(). It requires at least two arguments: a clustering, and a tree model. In this case we need to be careful about the missing values. 

confus(hcl1.99[!is.na(depth)],tree1)
$confus
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]   36    1    0    0    0    0    0    0
[2,]    5   30    1    0    0    3    1    0
[3,]    0    2   10    0    1    0    0    0
[4,]    0    1    0    0    0    1    0    0
[5,]    0    0    0    0   13    0    0    0
[6,]    0    1    0    0    0   30    0    0
[7,]    0    0    0    0    0    0    7    0
[8,]    0    1    1    0    0    0    0    0

$correct
[1] 126

$percent
[1] 0.8689655

$kappa
[1] 0.8342359
The actual values are given as rows, and the predicted values columns. You can see some confusion between types 1 and 2 (13+6=19 errors) and you can see where the missing types (4 and 8) are allocated.

In addition, confus() provides the number of correct predictions, the percent correct predictions, and the \(\kappa\) statistic.

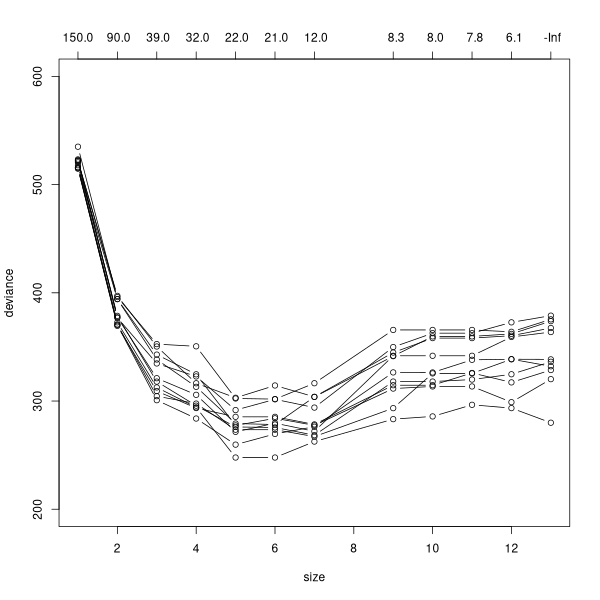
As for our experience modeling species with trees, the trees are over-fit and need to be pruned by cross-validation. 

plot(cv.tree(tree1),type='b',ylim=c(200,600))
for (i in 1:10) {
     x <- cv.tree(tree1)
     points(x$size,x$dev,type='b')
}



tree1.5 <- prune.tree(tre1,best=5)
tree1.5
summary(tree1.5)



tree1.5
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 145 501.900 2 ( 0.25517 0.27586  ... 0.01379 0.08966 0.21379 0.04828 0.01379 )  
   2) elev < 7980 83 273.200 6 ( 0.00000 0.18072  ... 0.15663 0.37349 0.08434 0.02410 )  
     4) elev < 7580 34  87.550 3 ( 0.00000 0.14706  ...0.38235 0.00000 0.00000 0.05882 )  
       8) elev < 6980 14   7.205 5 ( 0.00000 0.00000  ...0.00000 0.00000 0.00000 ) *
       9) elev > 6980 20  41.320 3 ( 0.00000 0.25000  ... 0.00000 0.00000 0.10000 ) *
     5) elev > 7580 49  95.200 6 ( 0.00000 0.20408  ... 0.00000 0.63265 0.14286 0.00000 )  
      10) slope < 2.5 20  48.230 2 ( 0.00000 0.40000  ... 0.00000 0.20000 0.35000 0.00000 ) *
      11) slope > 2.5 29  14.560 6 ( 0.00000 0.06897  ... 0.00000 0.93103 0.00000 0.00000 ) *
   3) elev > 7980 62  83.610 1 ( 0.59677 0.40323  ... 00000 0.00000 0.00000 0.00000 0.00000 ) *
Classification tree:
snip.tree(tree = tree1, nodes = c(11L, 9L, 10L, 3L))
Variables actually used in tree construction:
[1] "elev"  "slope"
Number of terminal nodes:  5 
Residual mean deviance:  1.392 = 194.9 / 140 
Misclassification error rate: 0.331 = 48 / 145 



confus(hcl1.99[!is.na(depth)],tree1.5)


 $confus
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]   37    0    0    0    0    0    0    0
[2,]   25    8    5    0    0    2    0    0
[3,]    0    0   12    0    1    0    0    0
[4,]    0    1    1    0    0    0    0    0
[5,]    0    0    0    0   13    0    0    0
[6,]    0    4    0    0    0   27    0    0
[7,]    0    7    0    0    0    0    0    0
[8,]    0    0    2    0    0    0    0    0

$correct
[1] 97

$percent
[1] 0.6689655

$kappa
[1] 0.5804702


 




How about our other classification using optpart?

tree2 <- tree(factor(opt5$clustering) ~ elev + av + slope + depth + pos)
plot(tree2)
text(tree2)




tree2


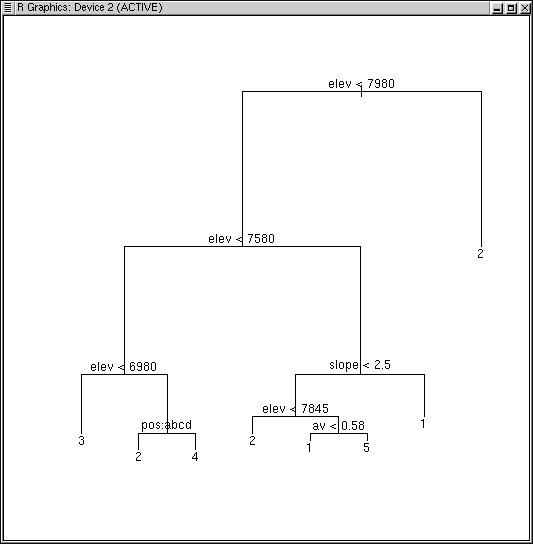
node), split, n, deviance, yval, (yprob)
      * denotes terminal node

 1) root 145 326.600 2 ( 0.25517 0.57931 0.08966 0.04828 0.02759 )  
   2) elev < 7980 83 225.300 1 ( 0.44578 0.26506 0.15663 ... 0.04819 )  
     4) elev < 7580 34  71.970 2 ( 0.00000 0.41176 0.38235 ... 0.00000 )  
       8) elev < 6980 14   7.205 3 ( 0.00000 0.07143 0.92857 ... 0.00000 ) *
       9) elev > 6980 20  25.900 2 ( 0.00000 0.65000 0.00000 ... 0.00000 )  
        18) pos: bottom,low_slope,mid_slope,ridge 12   6.884 2 ( 0.00000
                                    0.91667 0.00000 0.08333 0.00000 ) *
        19) pos: up_slope 8   8.997 4 ( 0.00000 0.25000 ... 0.00000 ) *
     5) elev > 7580 49  69.830 1 ( 0.75510 0.16327 0.00000  ... 0.08163 )  
      10) slope < 2.5 20  42.200 1 ( 0.40000 0.40000 0.00000 ... 0.20000 )  
        20) elev < 7845 10  12.220 2 ( 0.30000 0.70000 ... 0.00000 ) *
        21) elev > 7845 10  18.870 1 ( 0.50000 0.10000  ... 0.40000 )  
          42) av < 0.58 5   5.004 1 ( 0.80000 0.00000  ... 0.20000 ) *
          43) av > 0.58 5   9.503 5 ( 0.20000 0.20000 ... 0.60000 ) *
      11) slope > 2.5 29   0.000 1 ( 1.00000 0.00000  ... 0.00000 ) *
   3) elev > 7980 62   0.000 2 ( 0.00000 1.00000  ... 0.00000 0.00000 ) *


The tree is a little simpler, but there are only 5 types to predict instead of 8.

summary(tree2)


Classification tree:
tree(formula = factor(opt5$clustering) ~ elev + av + slope + depth + 
    pos)
Variables actually used in tree construction:
[1] "elev"  "pos"   "slope" "av"   
Number of terminal nodes:  8 
Residual mean deviance:  0.3636 = 49.81 / 137 
Misclassification error rate: 0.06897 = 10 / 145



The accuracy is a little higher (0.06897 misclassification), but there 
are fewer types so we would expect that.  The tree uses the same 4 out of 5
variables, with elevation (elev) again playing the dominant role.
Again, we need to cross-validate.


plot(cv.tree(tree2),type='b',ylim=c(100,400))
for (i in 1:10) {
    x <- cv.tree(tree2)
    points(x$size,x$dev,type='b')
}



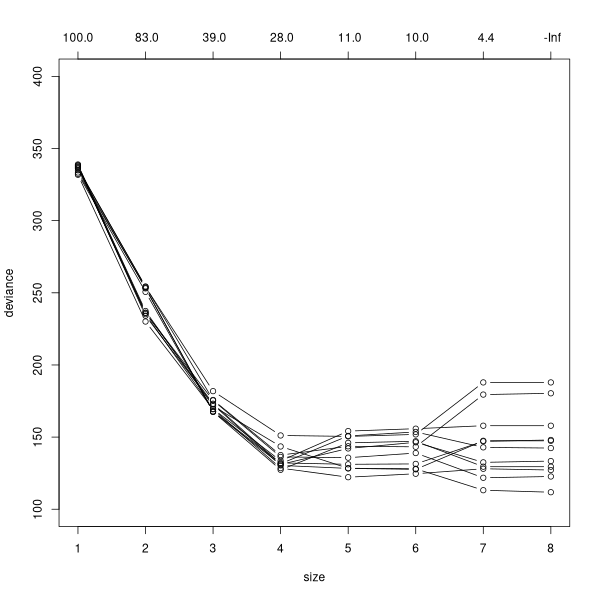Assuming (somewhat generously) that 6 is the best number:



tree2.6 <- prune.tree(tree2,best=6)
confus(opt5$clustering[!is.na(depth)],tree2.6)



$confus
     [,1] [,2] [,3] [,4] [,5]
[1,]   82    1    0    1    0
[2,]    3   34    0    0    0
[3,]    7    0    0    0    0
[4,]    0    0    0   13    0
[5,]    0    4    0    0    0

$correct
[1] 129

$percent
[1] 0.8896552

$kappa
[1] 0.8012337




Discussion


Predicting class membership for sample units based on environmental variables is
a common problem, commonly encountered in trying to draw a map of predicted
types in a GIS.  Tree classifiers work extremely well in such circumstances
because the trees can be converted to if/then statements in many languages used
in GIS applications.  In addition, the tree classifiers are actually pretty
good.

A very common alternative (which I will take up ASAP) is randomForest, or some
machine-learning algorithms such as maboost().


 Functions 


 confus <- function (clustering, model, diss = NULL) 
{
    clustering <- clustify(clustering)
    if (inherits(model, "tree")) {
        fitted <- predict(model)
    }
    else if (inherits(model, "randomForestest")) {
        fitted <- predict(model, type = "prob")
    }
    else if (inherits(model, "matrix")) {
        fitted <- model
    }
    numplt <- length(clustering)
    numclu <- length(levels(clustering))
    pred <- apply(fitted, 1, which.max)
    res <- matrix(0, nrow = numclu, ncol = numclu)
    for (i in 1:numplt) {
        res[clustering[i], pred[i]] <- res[clustering[i], pred[i]] + 
            1
    }
    if (!is.null(diss)) {
        part <- partana(clustering, diss)
        shunt <- diag(part$ctc)
        shunt[shunt == 0] <- 1
        tmp <- part$ctc/shunt
        fuzerr <- 1 - matrix(pmin(1, tmp), ncol = ncol(tmp))
        diag(fuzerr) <- 1
        fuzres <- res
        for (i in 1:ncol(res)) {
            for (j in 1:ncol(res)) {
                if (i != j) {
                  fuzres[i, j] <- res[i, j] * fuzerr[i, j]
                  fuzres[i, i] <- fuzres[i, i] + res[i, j] * 
                    (1 - fuzerr[i, j])
                }
            }
        }
        res <- fuzres
    }
    correct <- sum(diag(res))
    percent <- correct/numplt
    rowsum <- apply(res, 1, sum)
    colsum <- apply(res, 2, sum)
    summar <- sum(rowsum * colsum)
    kappa <- ((numplt * correct) - summar)/(numplt^2 - summar)
    out <- list(confus = res, correct = correct, percent = percent, 
        kappa = kappa)
    out
}




isolate <- function (mod,thresh=0.1)
{
    if (inherits(mod,'randomForest')) {
        tab <- mod$confus
    } else if (inherits(mod,'tree')) {
        tab <- confus(mod$y,mod)$confus
        rownames(tab) <- as.character(1:nrow(tab))
        colnames(tab) <- as.character(1:ncol(tab))
    } else {
        stop("Model type not recognized")
    }
    size <- nrow(tab)
   
    for (i in 1:(size-1)) {
        for (j in (i+1):size) {
            num <- tab[i,j] + tab[j,i]
            denom <- tab[i,i] + tab[j,j] +tab[i,j] + tab[j,i]
            if (denom > 0) {
                if (((tab[i,j] + tab[j,i]) / (tab[i,i] + tab[j,j] +tab[i,j] + tab[j,i]))
                          > thresh) {
                    a <- c(tab[i,i],tab[j,i])
                    b <- c(tab[i,j],tab[j,j])
                    out <- data.frame(a,b)
                    names(out) <- colnames(tab)[c(i,j)]
                    row.names(out) <- colnames(tab)[c(i,j)]
                    cat('\n')
                    print(out)
                }
            }
        }
    }
}