Lab 13 — Cluster Analysis

Cluster analysis is a multivariate analysis that attempts to form groups or "clusters" of objects (sample plots in our case) that are "similar" to each other but which differ among clusters. The exact definition of "similar" is variable among algorithms, but has a generic basis. The methods of forming clusters also vary, but follow a few general blueprints.

Similarity, Dissimilarity and Distance

Similarity is a characterization of the ratio of the number of attributes two objects share in common compared to the total list of attributes between them. Objects which have everything in common are identical, and have a similarity of 1.0. Objects which have nothing in common have a similarity of 0.0. As we have discussed previously (see Lab 8), there is a large number of similarity indices proposed and employed, but the concepts are common to all.

Dissimilarity is the complement of similarity, and is a characterization of the number of attributes two objects have uniquely compared to the total list of attributes between them. In general, dissimilarity can be calculated as 1 - similarity.

Distance is a geometric conception of the proximity of objects in a high dimensional space defined by measurements on the attributes. We've covered distance in detail under "ordination by PCO", and I refer you to that discussion for more details. Remember that R calculates distances with the dist function, and uses "euclidean", "manhattan", or "binary" as the "metric." The vegan package provides vegdist(), and labdsv provides dsvdis which together provide a large number of possible indices and metrics. Similar to the way in which these indices and metrics influenced ordination results, they similarly influence cluster analyses.

In practice, distances and dissimilarities are sometimes used interchangeably. They have quite distinct properties, however. Dissimilarities are bounded [0,1]; once plots have no species in common they can be no more dissimilar. Distances are unbounded on the upper end; plots which have no species in common have distances that depend on the number and abundance of species in the plots, and is thus variable.

Cluster Algorithms

Cluster algorithms are classified by two characteristics: (1) hierarchical vs fixed-cluster, and (2) if hierarchical, agglomerative vs divisive. We will explore agglomerative hierarchical clusters first, followed by fixed cluster and fuzzy fixed-cluster methods next.

In agglomerative hierarchical cluster analysis, sample plots all start out as individuals, and the two plots most similar (or least dissimilar) are fused to form the first cluster. Subsequently, plots are continually fused one-by-one in order of highest similarity (or equivalently lowest dissimilarity) to the plot or cluster to which they are most similar. The hierarchy is determined by the cluster at a height characterized by the similarity at which the plots fused to form the cluster. Eventually, all plots are contained in the final cluster at similarity 0.0

Agglomerative cluster algorithms differ in the calculation of similarity when more than one plot is involved; i.e. when a plot is considered for merger with a cluster containing more than one plot. Of all the algorithms invented, we will limit our consideration to those available in R, which are also those most commonly used. In R there are multiple methods:

In the "connected" or "single" linkage, the similarity of a plot to a cluster is determined by the maximum similarity of the plot to any of the plots in the cluster. The name "single linkage" comes because the plot only needs to be similar to a single member of the cluster to join. Single linkage clusters can be long and branched in high-dimensional space, and are subject to a phenomenon called "chaining", where a single plot is continually added to the tail of the biggest cluster. On the other hand, single linkage clusters are topologically "clean."

In the average linkage, the similarity of a plot to a cluster is defined by the mean similarity of the plot to all the members of the cluster. In contrast to single linkage, a plot needs to be relatively similar to all the members of the cluster to join, rather than just one. Average linkage clusters tend to be relatively round or ellipsoid. Median or centroid approaches tend to give similar results.

In the "complete" linkage, or "compact" algorithm, the similarity of a plot to a cluster is calculated as the minimum similarity of the plot to any member of the cluster. Similar to the single linkage algorithm, the probability of a plot joining a cluster is determined by a single other member of a cluster, but now it is the least similar, not the most similar. Complete linkage clusters tend to be very tight and spherical, thus the alternative name "compact."

Hierarchical Cluster Analysis in R

To perform cluster analysis you will want to load two packages: cluster and optpart. cluster is a package originally contributed by Kauffmann, but now maintained by Maechler et al. (2019). This package includes many of the famous algorithms ffrom Kaufman and Rousseeuw in their text "Finding Groups in Data." optpart is by Roberts and includes the algorithms featured in Roberts (2015).

In R, we typically use the hclust() function to perform hierarchical cluster analysis. hclust() will calculate a cluster analysis from either a similarity or dissimilarity matrix, but plots better when working from a dissimilarity matrix. We can use any dissimilarity object from dist(), vegdist(), or dsvdis().

Give the hclust() function the dissimilarity object as the first argument, and the method or metric as the second explicit argument. E.g.

hcl.avg <- hclust(demodist,"average")
To see the cluster analysis, simply use the plot().
plot(hcl.avg)

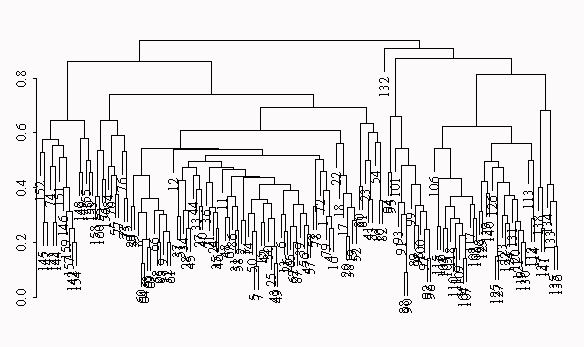
The hierarchical cluster analysis is drawn as a "dendrogram", where each fusion of plots into a cluster is shown as a horizontal line, and the plots are labeled at the bottom of the graph (although often illegibly in dense graphs).

I prefer a more traditional representation where the lines come all the way down. You can get that with

plot(hcl.avg,hang=-1,labels=NA)

The cluster analysis can be "sliced" horizontally to produce unique clusters either by specifying a similarity or the number of clusters desired. For example, to get 5 clusters, use

avg.5 <- slice(hcl.avg,k=5)
Then, to label the dendrogram with the group IDs, use
plot(hcl.avg, labels = as.character(hcl.5$clustering))

Given the clusters, you can use the cluster IDs (in our case avg.5) as you would any categorical variable. For example, 

table(berrep,avg.5$clustering)
      1  2  3  4 5 
   0 39 21 14 17 1
 0.5  0 47  0  0 0
   3  0 20  0  0 0
37.5  0  1  0  0 0
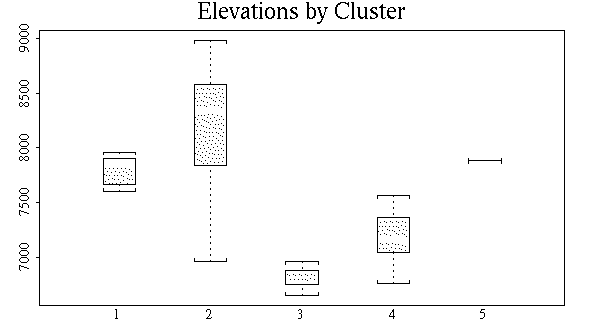
Where you can see that Berberis repens only occurs in cluster 2, but that cluster 2 also contains 21 plots without Berberis.

You can also perform environmental analyses of the clusters using the various plotting techniques we have developed. For example, to look at the distribution of plot elevations within clusters, we can do a boxplot as follows (assuming that the site data are already attached):

boxplot(elev~avg.5t$clustering)

As another example, I'll use complete on the Bray/Curtis dissimilarity calculated in a previous lab and then follow with const()

hcl.comp <- hclust(dis.bc,"complete")

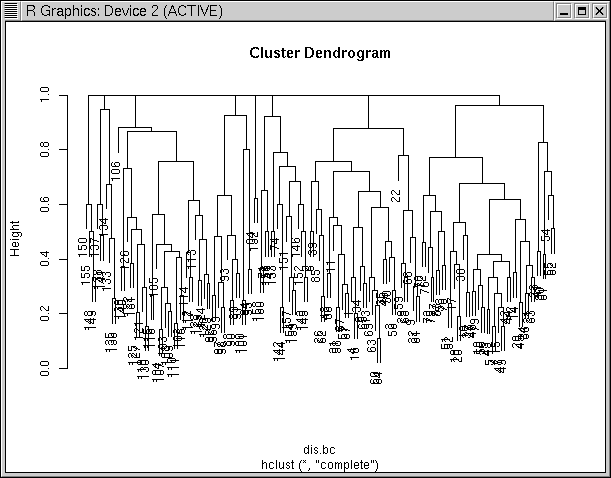
Notice how in the "complete" dendrogram clusters tend to hang from the 1.0 dissimilarity line. This is because the similarity of each cluster to the others is defined by the least similar pairs among the two, which is often complete dissimilarity. If we cut this at 0.99, we get 8 clusters that are distinct. 

hcl.comp.99 <- cutree(hcl.comp,h=0.99)

R version 4 broke some code in optpart, so to use const(), importance() or concov() you need to paste the functions in from down below. const() shows the constancy (fraction of sample units where a species is present) by type. The argument min= specifies the minimum constancy for a species' constancy to show up in the table, allowing you to focus on common or dominant species. 

const(bryceveg,hcl.comp.99,min=0.2)

          1    2    3    4    5    6    7    8
ameuta 0.34 0.21  .    .    .    .    .    .  
arcpat 0.71 0.89 0.23  0.5  .    .    .   0.25
arttri  .    .    .    .   0.85  .    .   0.25
atrcan  .    .    .    .   0.92  .    .    .  
ceamar 0.52 0.84  .    .    .    .    .    .  
cermon  .   0.28 0.94  .    .    .    .   1.00
  .     .    .    .    .    .    .    .    .
  .     .    .    .    .    .    .    .    .
  .     .    .    .    .    .    .    .    .
senmul 0.60 0.47  .    .    .   0.78 0.28  .  
sphcoc  .    .    .    .   0.64  .    .    .  
swerad 0.26 0.32  .    .    .    .    .    .  
taroff  .    .    .    .    .    .   0.42  .  
towmin  .    .    .    1.0  .    .    .    .  
tradub  .    .    .    .   0.21 0.21  .    .

Flexible-Beta

In recent years many ecologists have expressed a preference for a hierarchical clustering algorithm call "flexible Beta" developed by Australian ecologists Lance and Williams (1966). Lance and Williams determined that since all hierarchical agglomerative algorithms operate similarly, but differ in the calculation of multi-member dissimilarity, that it was possible to generalize the algorithms to a single algorithm with four parameters, alpha_1, alpha_2, beta, and gamma. Legendre and Legendre (1998) present a table (Table 8.8) that gives the L&W parameters to recreate many of the classical algorithms. Of more interest here is a special case where alpha_1 = alpha_2 = 0.625, beta = -0.25, and gamma = 0. Observe that not only are alpha_1 and alpha_2 equal, but that it is also the case that beta = 1 - (alpha_1 + alpha_2). This set of parameters gives a good intermediate result. To use flexible-beta in R you must load the package "cluster." This package contains several other functions we will want. Package "cluster" is loaded automatically by package "optpart", but if you have not loaded either yet
library(cluster)
The function we want to use is called agnes() (an abbreviation for agglomerative nesting). To perform a flexible-beta using agnes(), the call is a little more complicated than we have seen for other clustering algorithms). We need to specify alpha_1, alpha_2, beta, and beta in the call, using the par.method argument.
demoflex <- agnes(dis.bc,method='flexible',par.method=c(0.625,0.625,-0.25))
The defaults, however, are that alpha_1 = alpha_2, beta = 1 - (alpha_1 + alpha_2), and gamma = 0. So we can simply specify alpha_1 and get the desired results.
demoflex <- agnes(dis.bc,method='flexible',par.method=0.625)

Alternatively, package optpart has a wrapper fopr agnes() to get flexible-\(\beta\) the way ecologists usually refer to it. 

hcl.fb <- flexbeta(dis.bc,beta=-0.25)
plot(hcl.fb,hang=-1,labels=FALSE)

Cluster Utilities and Cluster Validity Indices

Hierarchical clustering can be challenging to manage. You not only have to decide: (1) what distance/dissimilarity to use, (2) which algorithm to use, but also (3) where to cut the dendrogram to produce clusters. Finally, when you are done, you need to evaluate the goodness-of-clustering. In combination, packages :cluster" and "optpart" can be very helpful here. First let's talk about goodness-of-clustering tests.
Goodness-of-Clustering
Aho et al. (2008) characterize goodness-of-clustering test as falling into two groups: internal and external. Internal tests are based on the distance/dissimilarity matrices that were used to create the partition, whereas external tests are based on data outside the construction of the dendrogram or the partition, such as environmental variables. In this section I will emphasize internal evaluators. P.J. Rousseeuw (1987) developed a diagnostic called "silhouette plots" that show the goodness-of-fit of each cluster member to the cluster and the hoomogeneity of each cluster. The graphic and statistic is based "silhouette width." \[ s_i = (b_i - a_i) / \max(a_i,b_i)\] where \(s_i\) is the silhouette width of sample unit \(i\), \(a_i\) is the mean dissimilatrity of sample unit \(i\) to its assigned cluster, and \(b_i\) is the mean dissimilarity of sample unit \(i\) to the cluster it is least dissimilar to (nearest neighbor cluster) aside from the one it is assigned to. \[s_i \sim [-1,1]\] Sample units that are less dissimilar to their assigned cluster than to their nearest neighbor have positive silhouette widths, and sample units that are less dissimilar to their nearest neighbor then to their assigned cluster have negative silhouette widths, and can be considered "mis-fits." To plot a silhouette plot yu need (12) a cluster solution, and (2) a distance/dissimilarity matrix.
plot(silhouette(hcl.5,dis.bc))
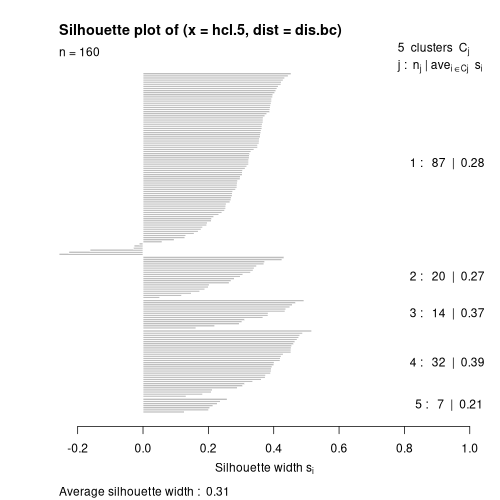What you see is (1) cluster 1 has 87 members with a mean width of 0.28, cluster 2 has 20 members with a mean width of 0.27, etc., and that the overall mean cluster width is 0.31 (which is pretty good). You also see that cluster 1 has several negative silhouette widths (or "reversals") and that maybe some plots are mis-assigned. You can compare results of other cluster solutions by comparing (1) the mean silhouette width, and (2) the number of reversals. Roberts (see Aho et al. 2008) proposed "partition analysis" as a way to evaluate partitions. It calculates (1) the mean similarity of each element to each cluster, (2) the mean similarity of each cluster to itself and every other cluster, and (3) importantly, the ratio of within-cluster similarity to between cluster similarity.
summary(partana(avg.5,dis.bc))
Number of clusters =  5 

 1  2  3  4  5 
87 20 14 32  7 

           [,1]        [,2]       [,3]       [,4]        [,5]
[1,] 0.37692189 0.115167420 0.01784878 0.05814787 0.051498315
[2,] 0.11516742 0.364767129 0.04080794 0.04945133 0.009980879
[3,] 0.01784878 0.040807939 0.42732677 0.09399166 0.033791447
[4,] 0.05814787 0.049451332 0.09399166 0.48048127 0.127317729
[5,] 0.05149832 0.009980879 0.03379145 0.12731773 0.318411602

Ratio of Within-cluster similarity/Among-cluster similarity =  5.954
That ratio of 5.954/1 is very good! There is also a plot() function to visualize the results, which plots two panels.
plot(partana(avg.5,dis.bc))
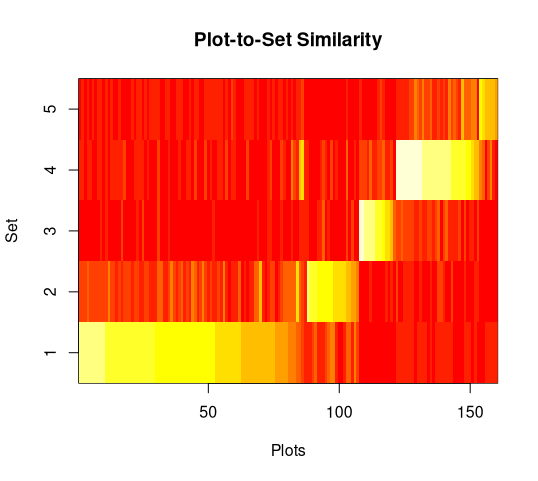The first panel shows the similarity of each sample unit to each cluster, with high similarities in white or yellow and low similarities in red. Sample units are sorted in order of their similarity to their assigned cluster. In this example yu can see that a few sample units assigned to cluster 1 are more similar to cluster 4 than they are to cluster 1, but that over all the results are pretty good (bright yellow on the diagonal and red off the diagonal). 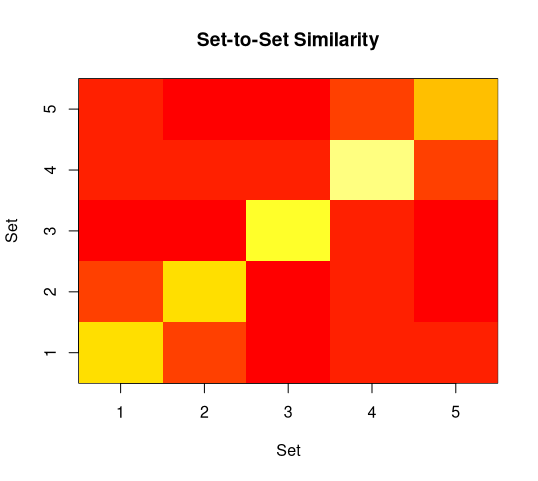The second panel ignores the individual sample units and just displays cluster means. You can see a slight similarity of cluster 1 to cluster 2 (faint orange off the diagonal), that cluster 4 and 5 are slightly similar (same criterion), and that cluster 4 has the highest homogeneity (brightest yellow) while cluster is not so good.
Selecting the Number of Clusters
Now that you have seen the silhouette width and partana ratio goodness-of-clustering analyses, you have a basis to compare different clustering results, including the best number of clusters. To facilitate that, the optpart package ahs the stride() command. stride() slices a dendrogram at as many points as desired, using an R sequence to specify. For example
avg.3.10 <- stride(3:10,hcl.avg)
The resulting stride object can then be analyzed by silhouette width or partana ratio.
silhouette(avg.3.10,dis.bc)
  clusters sil_width
1        3 0.2754676
2        4 0.2971435
3        5 0.3066199
4        6 0.2906381
5        7 0.2753434
6        8 0.2747093
7        9 0.2778687
8       10 0.2438136
Based on this output, you might choose five clusters as the best solution.
partana(avg.3.10,dis.bc)
  clusters    ratio
1        3 6.246947
2        4 5.924215
3        5 5.953795
4        6 5.936849
5        7 5.599706
6        8 5.596239
7        9 5.569672
8       10 5.519177
Partana analysis, however, prefers three clusters, which five clusters is pretty good. To help visualize these results, there is a plot() function that combines the silhouette width and partana ration is a single plot.
plot(avg.3.10,dis.bc)
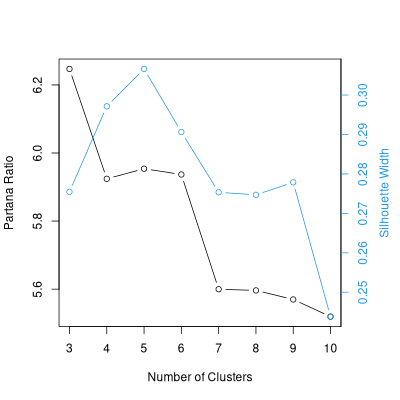Given this results, 3 or 5 cluster looks good, and there is no reason to prefer 4 or 6 over those two, and certainly higher numbers of clusters give poorer results.

Fixed-cluster Algorithms or Partitions

In contrast to hierarchical methods, in fixed-cluster algorithms (e.g. C-means, K-means or K-medoids), the number of clusters is specified a priori by the analyst, and the clusters are formed from either an initial guess at the cluster centers, or from random initial conditions. The clusters are not hierarchical, but rather form a direct partition of the data. The "goodness-of-fit" criterion (also called "stress") is generally some measure of within-cluster homogeneity versus among-cluster heterogeneity, often measured by the distance of each plot to the center of the cluster to which it belongs, compared to the average distance to other clusters.

In practice, you often don't know the best number of clusters a priori, and the approach adopted is to cluster at a range of values, comparing the stress values to find the best partition. Often, clustering with the same number of clusters but a different initial guess will lead to a different final partition, so replicates at each level are often required.

The original function for fixed-cluster analysis was called "K-means" and operated in a Euclidean space. Kaufman and Rousseeuw (1990) created a function called "Partitioning Around Medoids" (PAM) which operates with any of a broad range of dissimilarities/distance. To perform fixed-cluster analysis in R we'll use the pam() function from the cluster library. pam uses a distance matrix output from any of our distance functions, or a raw vegetation matrix (invoking dist() on the fly). I've had better luck explicitly creating a distance matrix first, and then submitting it to pam. 

pam.5 <- pam(dis.bc,k=5)
attributes(pam.5)

$names:
[1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
[6] "clusinfo"   "silinfo"    "diss"       "call"     
 
$class:
[1] "pam"       "partition"
The plots which serve as cluster centers (or medoids) are indicated by pam.5$medoids
pam.5$medoids
[1] "bcnp_64" "bcnp__7" "bcnp103" "bcnp159" "bcnp_88"
The cluster membership for each plot is given by
pam.5$clustering
bcnp__1 bcnp__2 bcnp__3 bcnp__4 bcnp__5 bcnp__6 bcnp__7 bcnp__8 
      1       1       1       1       2       1       2       2 
bcnp__9 bcnp_10 bcnp_11 bcnp_12 bcnp_13 bcnp_14 bcnp_15 bcnp_16 
      1       2       2       2       1       2       2       1 
      .       .       .       .       .       .       .       .
      .       .       .       .       .       .       .       .
      .       .       .       .       .       .       .       .
bcnp145 bcnp146 bcnp147 bcnp148 bcnp149 bcnp150 bcnp151 bcnp152 
      4       4       4       4       4       4       4       4 
bcnp153 bcnp154 bcnp155 bcnp156 bcnp157 bcnp158 bcnp159 bcnp160 
      4       4       4       4       4       4       4       4
There is a special plotting function for outputs from the cluster library, including pam(). In R, just plot the pam object.
plot(pam.5)

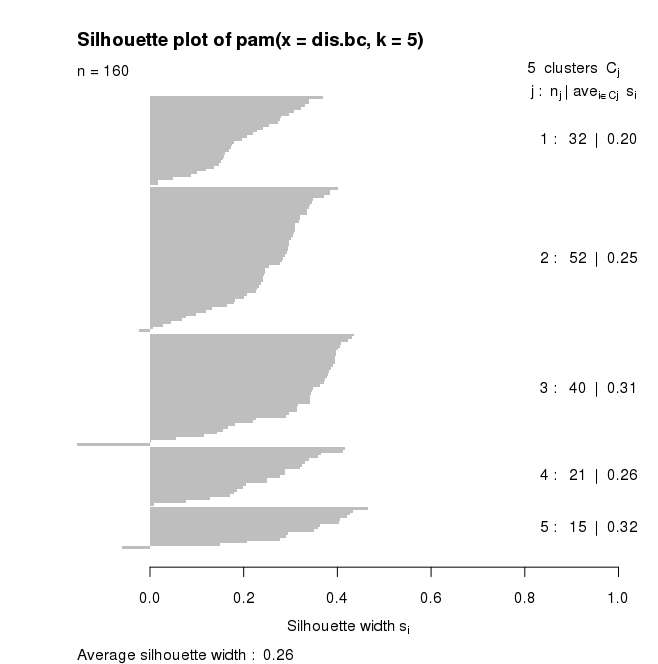
for pam(), the default plot is a silhouette plot.

Plots which fit well within their cluster have a large positive Silhouette width; those which fit poorly have a small positive or even a negative Silhouette.

The $clustering values can be used just as the "cut" values from the hierarchical cluster analysis before. For example,

boxplot(elev~pam.5$clustering)

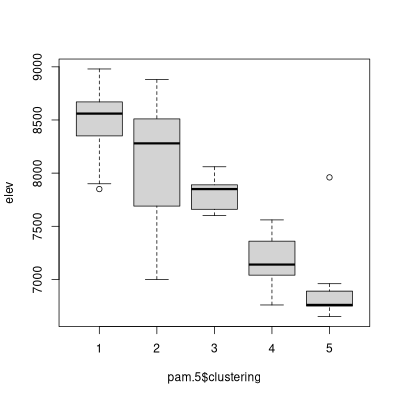
The two algorithms can be compared as follows:

table(avg.5$clustering,pam.5$clustering)
     1  2  3  4  5
  1 30 52  4  1  0
  2  0  0  0 20  0
  3  0  0  0  0 14
  4  0  0 32  0  0
  5  2  0  4  0  1
which shows that both algorithms found a similar cluster structure, but that pam() broke cluster 1 of avg.5 into two clusters. More infotmation can be obtained with the optpart functionclassmatch. 
match <- classmatch(avg.5,pam.5)
match
There is quite a bit of output, soI'll break it up here, but usually it all comes out at once. 
match
$tab
     pam.5
avg.5  1  2  3  4  5
    1 30 52  4  1  0
    2  0  0  0 20  0
    3  0  0  0  0 14
    4  0  0 32  0  0
    5  2  0  4  0  1

$pairs
   row column  n
1    1      2 52
2    4      3 32
3    1      1 30
4    2      4 20
5    3      5 14
6    1      3  4
7    5      3  4
8    5      1  2
9    1      4  1
10   5      5  1
The first table is familar; we just saw that fron the table function. The second table breaks down the tabkle by ropws and colum in the order of matches. You can see that it takes 10 pairs to catch all the matches.

The next table gives you the partial match at each step of filling out he previous table. 

$partial
 [1] 0.32500 0.52500 0.71250 0.83750 0.92500 0.95000 0.97500 0.98750
 [9] 0.99375 1.00000
The next table is not much to look at, but is helpful in structuring data sometimes. 
$ord
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    1    6    9    0
[2,]    0    0    0    4    0
[3,]    0    0    0    0    5
[4,]    0    0    2    0    0
[5,]    8    0    7    0   10
The last table is quite interesting. It gives our the membership of each sample unit in each of the new "merged" clusters so you can see which units stayed in the original class and which ones were "problematic". 
$combo
  [1]  3  3  3  3  1  3  1  1  3  1  1  1  3  1  1  3  1  1  1  1  1
 [22]  3  1  1  1  3  1  1  3  3  1  3  1  3  3  1  1  1  3  1  6  1
 [43]  1  1  1  1  1  3  1  1  1  1  1  1  1  3  1  1  3  3  3  3  3
 [64]  3  3  3  1  3  3  1  4  1  1  9  1  1  1  1  1  6  6  1  1  1
 [85]  3  3  1  5  5  5  5  5  5  5  5  5  5  5  5  5  5  2  2  2  2
[106]  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2
[127]  2  2  2  2  2  6  7  7  7  7 10  8  2  2  8  4  4  4  4  4  4
[148]  4  4  4  4  4  4  4  4  4  4  4  4  4

attr(,"class")
[1] "classmatch"
attr(,"type")
[1] "full"

New Non-Hierachical Cluster Algorithms

Roberts (2015) introduced two new non-hierarchical algorithms called optpart() and optsil. They had been in package optpart for many years but never published.

optpart() and optsil are, like K-means, re-allocation algorithms. This means you start off with an initial partition, and then iteratively reassign sample units from one cluster to another to optimize a goodness-of-clustering criterion. Not surprisingly, optpart() optimizes the partana ratio, and optsil() optimizes silhouette widths.

optpart() and optsil can be run in either of two approaches: (1) you can start with a random configuration, or (2) you can start with the results of another cluster analysis and "polish" the results. If starting from a random configuration, you probably want to start from numerous starts and keep the best results. Here's an example with optpart() 

opt.5 <- optpart(5,dis.bc)
summary(opt.5)
Number of clusters =  5 

 1  2  3  4  5 
12 14 38 92  4 

           [,1]       [,2]       [,3]       [,4]       [,5]
[1,] 0.44024149 0.04602221 0.04753422 0.09648594 0.01069798
[2,] 0.04602221 0.42732677 0.08550955 0.01790267 0.04115028
[3,] 0.04753422 0.08550955 0.40820806 0.05513161 0.07337579
[4,] 0.09648594 0.01790267 0.05513161 0.36012116 0.06023967
[5,] 0.01069798 0.04115028 0.07337579 0.06023967 0.21904762

Ratio of Within-cluster similarity/Among-cluster similarity =  6.528 in 37
iterations
You might recall that avgerage-linkage clustering gave us a partana ratio of 5.954. With one random start, optpart() achieved 6.528. Let's try 50 random starts. 
opt.5 <- bestopt(dis.bc,5,50)
Ratios for respective optparts 
 [1] 6.528 6.376 6.528 6.376 6.528 6.528 6.528 6.376 6.528 6.528 6.528
[12] 6.528 6.528 6.382 6.528 6.528 6.528 6.528 6.528 6.376 6.528 6.528
[23] 6.528 6.528 6.528 6.528 6.528 6.528 6.528 6.528 6.528 6.528 6.528
[34] 6.376 6.376 6.528 6.528 6.528 6.528 6.528 6.528 6.528 6.376 6.528
[45] 6.528 6.528 6.528 6.528 6.528 6.528

Choosing #  25  ratio =  6.528
Unusually, the best result was so clear that all 50 attempts converged to the same result. That's a little unusual. Let's try starting it from the flexible-\(\beta\) result. 
fb.5 <- slice(hcl.fb,5)
summary(partana(fb.5,dis.bc))
Number of clusters =  5 

 1  2  3  4  5 
31 45 32 14 38 

           [,1]       [,2]       [,3]       [,4]       [,5]
[1,] 0.50286049 0.33445898 0.10643014 0.01414965 0.04821295
[2,] 0.33445898 0.53288949 0.16025466 0.01512236 0.04832595
[3,] 0.10643014 0.16025466 0.24271388 0.04331102 0.07499580
[4,] 0.01414965 0.01512236 0.04331102 0.42732677 0.08179415
[5,] 0.04821295 0.04832595 0.07499580 0.08179415 0.37590195

Ratio of Within-cluster similarity/Among-cluster similarity =  3.872
So we're starting from a partition with a ratio of 3.872. 
 opt.fb <- optpart(fb.5,dis.bc)
summary(opt.fb) 
Number of clusters =  5 

 1  2  3  4  5 
 4 92 12 14 38 

           [,1]       [,2]       [,3]       [,4]       [,5]
[1,] 0.21904762 0.06023967 0.01069798 0.04115028 0.07337579
[2,] 0.06023967 0.36012116 0.09648594 0.01790267 0.05513161
[3,] 0.01069798 0.09648594 0.44024149 0.04602221 0.04753422
[4,] 0.04115028 0.01790267 0.04602221 0.42732677 0.08550955
[5,] 0.07337579 0.05513161 0.04753422 0.08550955 0.40820806

Ratio of Within-cluster similarity/Among-cluster similarity =  6.528 in 37
iterations
So it appears we're back to the same result.

The default plot() for anoptpat() is of course a partana plot. There is, however, third panel showing the progress of the optimization, show here for the opt.fb result. 

plot(opt.fb,panel=3)
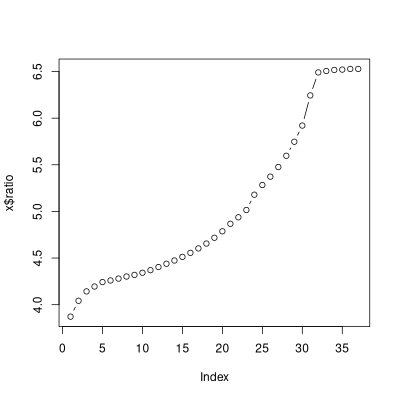optsil() can be run like optpart(). To generate a five-cluster optsil do 
sil.5 <- optsil(5,dis.bc,maxitr=250)
sil.5
$clustering
  [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [33] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [65] 3 3 3 3 3 3 2 3 3 1 3 3 3 3 3 4 4 3 3 3 3 3 3 5 5 5 5 5 5 2 2 5
 [97] 5 5 5 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
[129] 4 4 4 2 4 2 4 4 2 2 4 4 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

$sils
  [1] -0.0383837682 -0.0360490476 -0.0340548649 -0.0320981517
  [5] -0.0304199390 -0.0287459436 -0.0273244130 -0.0259370161
  [9] -0.0245875431 -0.0232583180 -0.0217805101 -0.0201710721
        .             .             .             .
        .             .             .             .
        .             .             .             .
[157]  0.2963449791  0.2989026435  0.3013503421  0.3035480820
[161]  0.3051924764  0.3070876618  0.3094570117  0.3109986270
[165]  0.3117793881  0.3121004686  0.3122590125  0.3126651665

$numitr
[1] 168

attr(,"class")
[1] "optsil"     "clustering"
attr(,"call")
optsil.default(x = 5, dist = dis.bc, maxitr = 250)
attr(,"timestamp")
[1] "Mon Mar 29 03:50:35 2021"

plot(silhouette(sil.5,dis.bc))
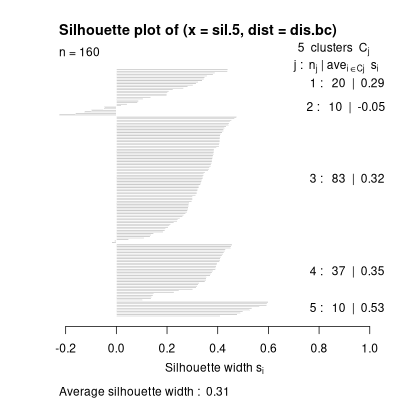optsil() can be slow to converge. In this case I specified a maximum of 250 iterations and it ran for 168. Often the best idea is to start optsil() from another cluster solution as the initial conditions. 
sil.fb.5 <- optsil(fb.5,dis.bc)
sil.fb.5

$clustering
  [1] 1 1 1 1 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 2 2 1 1 2 2 1 2 2 1 1 2 1
 [33] 2 1 1 2 2 2 1 2 2 2 2 2 2 1 2 1 2 2 2 2 2 2 2 1 2 2 1 1 1 1 1 1
 [65] 1 1 2 1 1 2 3 2 2 3 2 2 2 2 2 5 5 2 2 2 1 1 2 4 4 4 4 4 4 4 4 4
 [97] 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
[129] 5 5 5 1 5 1 5 5 1 1 5 5 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3

$sils
 [1] 0.2537863 0.2560616 0.2573747 0.2585516 0.2595028 0.2602953
 [7] 0.2608121 0.2618873 0.2625571 0.2629374 0.2635494 0.2641968
[13] 0.2645527 0.2650535 0.2655142 0.2655312

$numitr
[1] 16

attr(,"class")
[1] "optsil"     "clustering"
attr(,"call")
optsil.default(x = fb.5, dist = dis.bc)
attr(,"timestamp")
[1] "Mon Mar 29 04:00:18 2021"

par(mfrow=c(1,2))
plot(silhouette(fb.5,sdis.bc))
plot(silhouette(sil.fb.5,dis.bc))
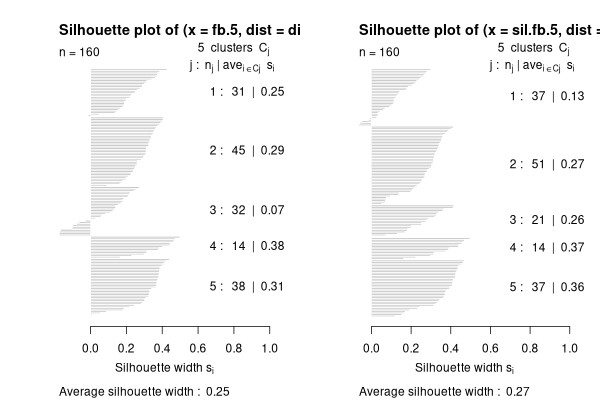You can see that optsil() improved the silhouette width from 0.25 to 0.27. That's not great. 
sil.opt.5 <- optsil(opt.5,dis.bc)
par(mfrow=c(1,2))
plot(silhouette(opt.5.dis.bc))
plot(silhouette(sil.opt.5.is.bc))
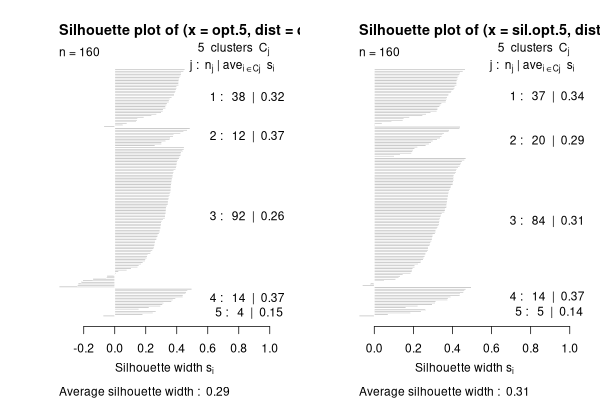. That's a littlr better.
Using stride()
It's possible to use the stride function with optpart() or . With optpart() you can proceed directly, by passing a dissimilarity matrix and the argument "type='optpart'" 
opt.2.10 <- stride(2:10,dis.bc,type='opt')
Ratios for respective optparts 
 [1] 6.445 6.445 6.445 6.445 6.445 6.445 6.445 6.445 6.445 6.445

Choosing #  9  ratio =  6.445 
Ratios for respective optparts 
 [1] 6.286 6.404 6.278 6.286 6.286 6.278 6.286 6.546 6.278 6.286
     .     .     .     .     .     .     .    .    .    .     .
     .     .     .     .     .     .     .    .    .    .     .
     .     .     .     .     .     .     .    .    .    .     .
Choosing #  6  ratio =  6.534 
Ratios for respective optparts 
 [1] 4.488 6.534 6.534 4.481 6.534 4.485 4.307 6.534 6.534 4.473

Choosing #  8  ratio =  6.534 

plot(opt.2.10,dis.bc)
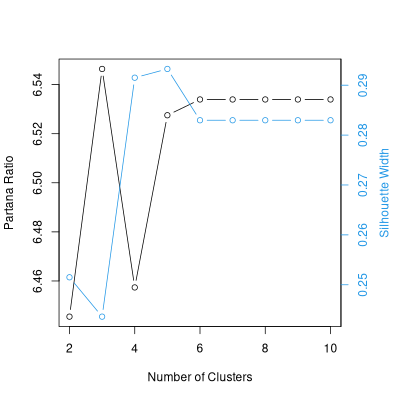With optsil you "polish" an existing stride. 
sil.2.10 <- optsil(opt.2.10,dis.bc)
plot(sil.2.10,dis.bc)
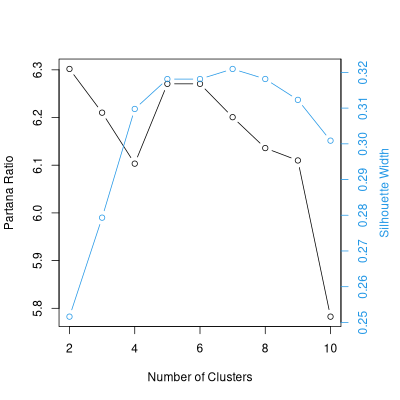
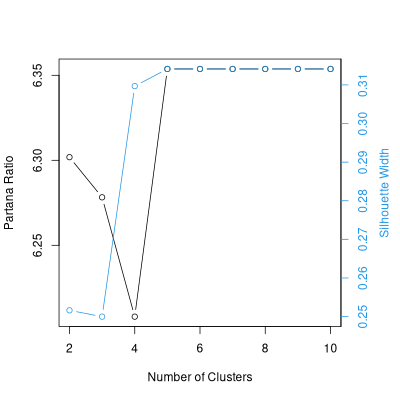As an alternative, here's a polish of the average linkage result. 
avg.sil.2.10 <- optsil(avg.2.10,dis.bc)
plot(avg.sil.2.10,dis.bc)

References

Aho, K., D.W. Roberts, and T.W.Weaver. 2008. Using geometric and non-geometric internal evaluators to compare eight vegetation classification methods. J. Veg. Sci. 19:549-562.

Kaufman, L. and P.J. Rousseeuw. Finding Groups in Data: An Introduction to Cluster Analysis.

Lance, G.N., and W.T. Williams (1966). A General Theory of Classificatory Sorting Strategies, I. Hierarchical Systems. Computer J. 9:373-380.

Legendre, P. and L. Legendre (1998). Numerical Ecology. Elsevier.

Lengyel, A., D.W. Roberts and Z. Botta-Dukat. 2021. Comparison of silhouette‐based reallocation methods for vegetation classification. J. Veg. Sci. 2021;32:e12984 https://doi.org/10.1111/jvs.12984

Maechler, M., Rousseeuw, P., Struyf, A., Hubert, M., Hornik, K.(2019). cluster: Cluster Analysis Basics and Extensions. R package version 2.1.0

Roberts, D.W. 2015. Vegetation classification by two new iterative reallocation optimization algorithms. Plant Ecol. Vol. 216(5):741-758.

Rousseeuw, P.J. (1987) Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. (20):53-65.

Library optpart

Library optpart is available at CRAN

Miscellaneous Scripts

const <- function (comm, clustering, minval = 0, show = minval, digits = 2, 
    sort = FALSE, spcord = NULL) 
{
    if (missing(clustering)) {
        const <- apply(comm > 0, 2, sum)/nrow(comm)
        const <- const[const >= minval]
        const <- data.frame(const)
        names(const) <- deparse(substitute(comm))
        return(round(const, digits))
    }
    else if (is.logical(clustering)) {
        comm <- comm[clustering, ]
        const <- apply(comm > 0, 2, sum)/nrow(comm)
        const <- const[const >= minval]
        const <- data.frame(const)
        names(const) <- deparse(substitute(clustering))
        return(round(const, digits))
    }
    clustering <- clustify(clustering)
    if (length(table(clustering)) == 1) {
        const <- apply(comm > 0, 2, sum)/nrow(comm)
        const <- const[const >= minval]
        const <- data.frame(const)
        return(round(const, digits))
    }
    else {
        res <- matrix(0, nrow = ncol(comm), ncol = length(levels(clustering)))
        x <- apply(comm, 2, function(x) {
            tapply(x > 0, clustering, sum)
        })
        y <- as.numeric(table(clustering))
        res <- x/y
        keep <- as.logical(apply(res, 2, max) >= minval)
        res <- res[, keep]
        tmp <- as.data.frame(t(res))
        row.names(tmp) <- names(comm)[keep]
        if (!is.null(spcord)) {
            tmp <- tmp[rev(order(spcord[keep])), ]
        }
        tmp <- format(round(tmp, digits = digits))
        tmp[tmp < show] <- substring(" .  ", 1, digits + 2)
        names(tmp) <- attr(clustering, "levels")
        attr(tmp, "call") <- match.call()
        attr(tmp, "timestamp") <- date()
        if (sort) {
            print(tmp)
            repeat {
                plots <- readline(" enter the species: ")
                if (plots == "") {
                  break
                }
                else {
                  pnt <- readline(" in front of        : ")
                }
                for (i in (strsplit(plots, ",")[[1]])) {
                  ord <- 1:nrow(tmp)
                  x <- match(i, row.names(tmp))
                  if (!is.na(x)) {
                    z <- ord[x]
                    ord <- ord[-x]
                    y <- match(pnt, row.names(tmp))
                    if (!is.na(y)) {
                      if (y > 1) {
                        first <- ord[1:(y - 1)]
                        last <- ord[y:length(ord)]
                        ord <- c(first, z, last)
                      }
                      else {
                        last <- ord[y:length(ord)]
                        ord <- c(z, last)
                      }
                      tmp <- tmp[ord, ]
                      print(tmp)
                    }
                    else {
                      print(paste("species", pnt, "does not exist"))
                    }
                  }
                  else {
                    print(paste("species", i, "does not exist"))
                  }
                }
            }
            return(tmp)
        }
    }
    return(tmp)
}


importance <- function (comm, clustering, minval = 0, digits = 2, show = minval, 
    sort = FALSE, typical = TRUE, spcord, dots = TRUE) 
{
    if (missing(clustering)) {
        impt <- apply(comm, 2, sum)/nrow(comm)
        impt <- impt[impt >= minval]
        impt <- data.frame(impt)
        names(impt) <- deparse(substitute(comm))
        return(round(impt, digits))
    }
    else if (is.logical(clustering)) {
        comm <- comm[clustering, ]
        impt <- apply(comm, 2, sum)/nrow(comm)
        impt <- impt[impt >= minval]
        impt <- data.frame(impt)
        names(impt) <- deparse(substitute(clustering))
        return(round(impt, digits))
    }
    clustering <- clustify(clustering)
    if (length(table(clustering)) == 1) {
        impt <- apply(comm, 2, sum)/nrow(comm)
        impt <- impt[impt >= minval]
        impt <- data.frame(impt)
        return(round(impt, digits))
    }
    else {
        res <- matrix(0, nrow = ncol(comm), ncol = length(levels(clustering)))
        x <- apply(comm, 2, function(x) {
            tapply(x, clustering, sum)
        })
        if (typical) {
            y <- apply(comm, 2, function(x) {
                tapply(x > 0, clustering, sum)
            })
        }
        else {
            y <- apply(comm, 2, function(x) {
                tapply(x >= 0, clustering, sum)
            })
        }
        y[x == 0] <- 1
        res <- x/y
        keep <- as.logical(apply(res, 2, max) >= minval)
        res <- res[, keep]
        tmp <- as.data.frame(t(res))
        row.names(tmp) <- names(comm)[keep]
        if (!missing(spcord)) {
            tmp <- tmp[rev(order(spcord[keep])), ]
        }
        if (dots) {
            tmpx <- format(round(tmp, digits = digits))
            tmpx[tmp < show] <- substring(" .  ", 1, nchar(tmpx[1, 
                1]))
            print(tmpx)
        }
        if (sort) {
            cat("\nConstancy Table\n\n")
            print(tmp)
            repeat {
                plots <- readline(" enter the species: ")
                if (plots == "") {
                  break
                }
                else {
                  pnt <- readline(" in front of        : ")
                }
                for (i in (strsplit(plots, ",")[[1]])) {
                  ord <- 1:nrow(tmp)
                  x <- match(i, row.names(tmp))
                  if (!is.na(x)) {
                    ord <- ord[-x]
                    y <- match(pnt, row.names(tmp[ord, ]))
                    if (!is.na(y)) {
                      if (y == 1) {
                        ord <- c(x, ord)
                      }
                      else {
                        first <- ord[1:(y - 1)]
                        last <- ord[y:length(ord)]
                        ord <- c(first, x, last)
                      }
                      tmp <- tmp[ord, ]
                      print(tmp)
                    }
                    else {
                      print(paste("species", pnt, "does not exist"))
                    }
                  }
                  else {
                    print(paste("species", i, "does not exist"))
                  }
                }
            }
            attr(tmp, "call") <- match.call()
            attr(tmp, "comm") <- deparse(substitute(comm))
            return(tmp)
        }
    }
}


concov <- function (comm, clustering, digits = 1, width = 5, typical = TRUE,
    thresh = 10)
{
    if (missing(clustering)) {
        const <- apply(comm > 0, 2, sum)/nrow(comm)
        keep <- const >= thresh/100
        impt <- apply(comm, 2, sum)/nrow(comm)
        a <- formatC(as.numeric(const) * 100, width = 2, format = "d")
        b <- formatC(as.numeric(impt), width = width, digits = digits,
            format = "f")
        tmp <- NULL
        tmp <- cbind(tmp, paste(a, "(", b, ")", sep = ""))
        tmp <- tmp[keep]
        tmp <- data.frame(tmp)
        row.names(tmp) <- names(comm)[keep]
        attr(tmp, "call") <- match.call()
        attr(tmp, "comm") <- deparse(substitute(comm))
        attr(tmp, "timestamp") <- date()
        return(tmp)
    } else if (is.logical(clustering)) {
        comm <- comm[clustering, ]
        comm <- comm[, apply(comm > 0, 2, sum) > 0]
        x <- apply(comm > 0, 2, sum)
        y <- apply(comm, 2, sum)/x
        x <- x/nrow(comm)
        keep <- apply(as.matrix(x), 1, max) >= thresh/100
        a <- formatC(as.numeric(x) * 100, width = 2, format = "d")
        b <- formatC(as.numeric(y), width = width, digits = digits,
            format = "f")
        tmp <- NULL
        tmp <- cbind(tmp, paste(a, "(", b, ")", sep = ""))
        tmp <- tmp[keep]
        tmp <- data.frame(tmp)
        row.names(tmp) <- names(comm)[keep]
        names(tmp) <- deparse(substitute(clustering))
        attr(tmp, "call") <- match.call()
        attr(tmp, "comm") <- deparse(substitute(comm))
        attr(tmp, "clustering") <- clustering
        attr(tmp, "timestamp") <- date()
        return(tmp)
    }
    clustering <- clustify(clustering)
    if (length(table(clustering))==1)  {
        const <- apply(comm > 0, 2, sum)/nrow(comm)
        keep <- const >= thresh/100
        impt <- apply(comm, 2, sum)/nrow(comm)
        a <- formatC(as.numeric(const) * 100, width = 2, format = "d")
        b <- formatC(as.numeric(impt), width = width, digits = digits,
            format = "f")
        tmp <- NULL
        tmp <- cbind(tmp, paste(a, "(", b, ")", sep = ""))
        tmp <- tmp[keep]
        tmp <- data.frame(tmp)
        row.names(tmp) <- names(comm)[keep]
        names(tmp) <- deparse(substitute(clustering))
        attr(tmp, "call") <- match.call()
        attr(tmp, "comm") <- deparse(substitute(comm))
        attr(tmp, "clustering") <- clustering
        attr(tmp, "timestamp") <- date()
        return(tmp)
    } else {
        levels <- levels(clustering)
        clustering <- as.integer(clustering)
        x <- const(comm, clustering)
        y <- importance(comm, clustering, typical = typical)
        tmp <- NULL
        keep <- apply(as.matrix(x), 1, max) >= thresh/100
        for (i in 1:length(table(clustering))) {
            a <- formatC(as.numeric(x[, i]) * 100, width = 2,
                format = "d")
            b <- formatC(as.numeric(y[, i]), width = width, digits = digits,
                format = "f")
            tmp <- cbind(tmp, paste(a, "(", b, ")", sep = ""))
        }
        tmp <- tmp[keep, ]
        tmp <- data.frame(tmp)
        row.names(tmp) <- names(comm)[keep]
        names(tmp) <- levels
        attr(tmp, "call") <- match.call()
        attr(tmp, "comm") <- deparse(substitute(comm))
        attr(tmp, "clustering") <- clustering
        attr(tmp, "timestamp") <- date()
        return(tmp)
    }
    tmp
}

remos <-  function(d,gr,lim=-0.001,method=c(1,2),
                 return.partitions=FALSE,max.iter=Inf)  
{
  # auth: Attila Lengyel
  gr_new <- gr
  o <-  -1
  z <- 1
  dw <- 1
  w <- u <- y <- vector('numeric')
  W <- matrix(NA, nrow=length(gr), ncol=0)
  parts <- vector('numeric')
  while(o < lim)  {
    SIL <- cluster::silhouette(gr_new,d)
    orig <- SIL[,1]
    neig <- SIL[,2]
    width <- SIL[,3]
    W <- cbind(W,width)
    if(method==1) worst <- which.min(width)
    if(method==2) worst <- which(width < lim)
    if(z > 1) dw <- as.vector(colSums((W-width)^2)[-z])
    o <- min(width)
    if(o < lim) {
     gr_new[worst] <- neig[worst]
    }
    y[z] <- o
    u[z] <- sum(width<0)
    w[z] <- abs(sum(width[width<0]))
    parts <- cbind(parts,gr_new)
    if(any(dw==0))   o <- lim+1
    if(z==max.iter) o <- lim+1
    z <- z+1
    }
  fin1 <- u==min(u)
  fin2 <- w==min(w[fin1]) & fin1
  gr_final <- parts[,fin2]

  if(return.partitions==TRUE) result <- list(gr_final,parts,y,u,w)
  if(return.partitions==FALSE) result <- list(gr_final,y,u,w)
  return(result)
}